
A Source
of Richness in the Main Themes of Samuel Barber's Violin Concerto and Piano
Concerto: Hierarchical Conflict and the Implication-Realization Model
Robert Maggio
In this paper I will analyze in detail the
main themes of Samuel Barber's Violin Concerto and Piano Concerto using
the theory of implication and realization. I will argue that melodic richness
and aesthetic effect correspond to the degree of cognitive hierarchical
conflict between higher and lower-level patterns. Since throughout the critical
study of the these melodies I shall employ the various symbols and signs of the
implication-realization theory, it will be beneficial at this point to the
reader to become familiar with the theory and its symbology.1
An Overview of the Implication-Realization Model
The implication-realization model hypothesizes that as we listen to
music we experience a dynamic interaction between cognitive constants
(subconscious reactions based on perceptions of grouping, similarity, and
differentiation) and learned expectations created from our knowledge of other
related music (extraopus style) or from our memory of
previous events within the individual work itself (intraopus
style) (Figure 1).

Figure 1: Interaction of Learning and Cognitive Constants
Three cognitive constants affect our perception of the three following
parameters: pitch, intervallic motion, and registral
direction.2 The constants are applied only
to one parameter at a time. The first of the three is one of similarity based
on Gestalt laws of common direction, similarity, and proximity. Thus, if A + A,
then a further A is implied, which means that sameness or similarity (A
+A) causes the subconscious expectation of more sameness or similarity (A), all
things being equal. The second constant is one of differentiation, a
hypothetical construct symmetrical to the Gestalt rules of similarity. Thus, if
A + B, then C is implied, which means that differentiation (A + B) causes the
expectation of more differentiation (C), all things being equal.3
The definitions of the first constants, (A + A → A and A + B → C), raise two important questions. First, how does the analyst define "similarity" and "differentiation" in musical items. And second, how does the analyst evaluate the meaning of such distinctions when the data are necessarily relative? The solution to these questions lies within the third theoretical constant, the syntactic parametric scale, which defines the relative terms "similarity" and "differentiation." The syntactic parametric scale hypothesizes that intervals from the unison through the P4 are small intervals that imply continuation, or similarity, of intervallic size (I) and registral direction (V) (up, down, or lateral). Intervals from the P5 through the M7 are larger intervals that imply reversal or differentiation, of intervallic size and registral direction (i.e. a small interval and a change of registral direction is expected after a large interval) (Figures 2 and 3). Given the relative nature of intervallic size, the analyst must consider that an interval's degree of implication is directly proportional to its size.
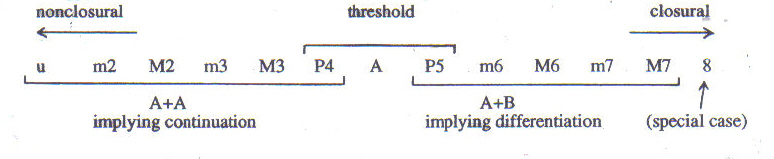
Figure
2: Syntactic Parametric
Scale
Figure 3: Continuation and Differentiation.
Five melodic archetypes derived from the theoretical constants form the basis of the system of melodic structures (Figure 4). The first two archetypes, process [P] and reversal [R] are direct analogues of the first two constants (similarity and differentiation, respectively.) A process [P] is a melodic structure with at least three pitches that have relations of similarity of intervallic size and registral direction between all the pitches. A reversal [R] is a melodic structure with three pitches that have relations of differentiation of intervallic size am:1 registral direction.

Figure
4: Synthetic example of
five melodic archetypes derived from the theoretical
constants
The third melodic archetype is the dyad, a
two-pitch structure symbolized by the arabic
numeral that corresponds to the size of the interval. This structure occurs
when closure on the second pitch denies further implication, due to metric
emphasis, harmonic resolution of dissonance, directional cumulation
or some combination of these.
The fourth melodic archetype is the monad
[M], a single-pitch structure that has neither implication nor realization
since implication is created by two pitches and realization by three pitches.
Monads are isolated pitches usually because they are followed by a silence
(i.e. the last pitch of a piece.)
The fifth and final melodic archetype is exact or near registral return [a b a; a b a1]. These symbols
indicate instances where a melody departs from a previously established pitch
[a], then returns, either to the same pitch [a] or one very close by [a1].
This archetype does not involve implication since the pitches so labeled need
not be successive.
The implication-realization model also proposes six melodic structures derived from the archetypes (Figures 5a + b). Duplications [ID] are derived from processes and consist of three or more repeated notes, where the implicative interval is the unison and the registral direction lateral. Sometimes only one parameter, interval or register is realized while the other is denied. For example, when the implicative interval implies continuation but the realization denies the expected intervallic size or registral direction, the resulting structures are called registral process [VP] and intervallic process [IP]. Just as duplications [D] are derived from processes [P], intervallic duplications [ID] are derived from intervallic processes [IP]. Intervallic duplication refers to the case where the intervallic differentiation is nil and registral implication is denied (i.e. the first and third tones of the structure are the same pitch, and the second is a different pitch.)

Figure 5a: A list of archetypal melodic structures and their derivatives

Figure 5b: Synthetic examples of the melodic structures
derived from the archetypes
When the implicative interval
implies differentiation but the realization denies registral
direction or intervallic motion, the resulting structures are called
intervallic reversal [IR] and registral reversal [VR]
respectively. Thus far, each of the implicative
archetypes and their derivatives have been discussed
in their prospective form. A structure is said to be prospective, for instance,
when the implicative interval is small and the terminal pitch reaffirms the
resulting structure to be of a

Figure 6: Synthetic examples of eight retrospective structures
A family tree
of melodic structures can be constructed, thoroughly accounting for the myriad
of basic melodic shapes found in all music (Figure 7).
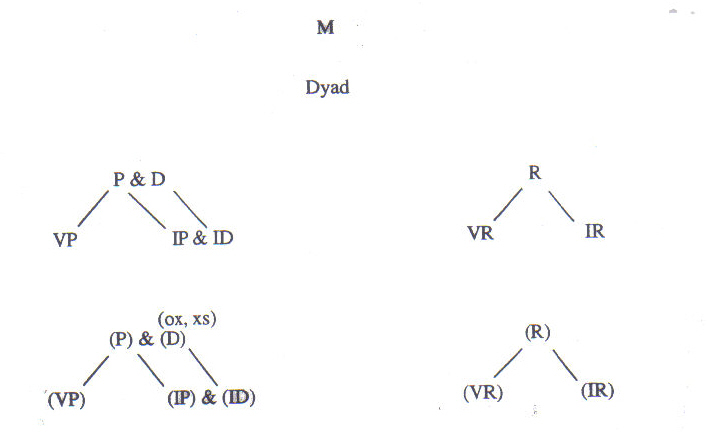
Figure 7: Family Tree of Melodic Structures
Rhythm and meter play a major role in the segmentation or
parsing of melody into structures, since an interval in a melody implies metric
and rhythmic placement as well as intervallic motion and registral
direction. Factors such as harmonic resolution of dissonance, placement on a
weak beat, and a counter-cumulative rhythmic position
can interfere with the closure of a structure and

![]()
Figure 8: Synthetic examples of harmonic resolution of
dissonance (x), placement on a weak
beat, and counter-cumulative (long-short) rhythmic
position causing compound structures
Finally, the analyst must address the
issue of transformation, the creation of hierarchical levels (conceptually
comparable to the foreground, middle-ground, and background of a Schenkerian analylsis.) The
initial tone and the terminal tone in a structure are those that transform to
the next level and form their own implication and realization on the next
level. Registral and intervallic activity on one
level is in some sense embodied in the next higher level. These interactions of
level contribute to the richness and subtlety of melodic cognition.
We began this discussion of the
implication-realization model, with the hypothesis that our cognitive constants
interact with prior learning when we listen to music. Hopefully the relevance
of this hypothesis to musical analysis has become clear to the reader. It
forces the analyst to clearly separate expectations created from style
knowledge from basic human pattern processing and further to provide empirical
evidence supporting any claim of style impingement.
Now let us turn to the specific issues involved with the application of the model to the melodies of Samuel Barber's piano and violin concerti.
Introduction
The
melodies analyzed in this critical study are presented in order of increasing
complexity and aesthetic affect.4 In this
paper, complexity corresponds to the degree of cognitive conflict between
embodiment of suppressed implication from
The main themes from the slow movements of
these works will serve as intermediary stages in the discussion of melodic
complexity and aesthetic affect. In both, clearly separated phrases develop
subtle motivic variations that create relatively
simple conflicts between high and low levels. Melodic dissonance in the slow
movement of the Piano Concerto creates a richness and complexity greater
than that found in the slow movement of the Violin Concerto. In the most
complex melody to be discussed in this study, that of the first movement of the
Violin Concerto, all structural hierarchies engage in an elaborate
intra- and inter-level dialogue, interlocking with one
another to seam an exquisite eleven-bar phrase.
Piano Concerto, First Movement, measures
19 -27.
Over the course of this melody,
hierarchical levels diminish in number and complexity (Example 1). The initial
angular leaps, contramodal dissonances on stressed
beats, and the unusual syncopation of the structural tones create intense
excitement in the first four bars (mm. 19-22). The second part of the melody
(mm. 23-24) is calmer because the melodic structures are simpler. Measures
25-27, the third section of the melody, are nearly "flat" (i.e. they
have very few transformational tones and create only two levels).
The main motive (a descending arpeggio) fights the meter with syncopation, thus shifting the transformational tones to weak beats (Example 2). Note the fortissimo entrance of the violins off the beat in measure 19, the metrically enveloping process [P]5, the sudden reversal [R] on the downbeat of measure 22 (see middle level), and the resolutions of the dyads [7] off the beat in measures 20 and 22 (see again Example 1).
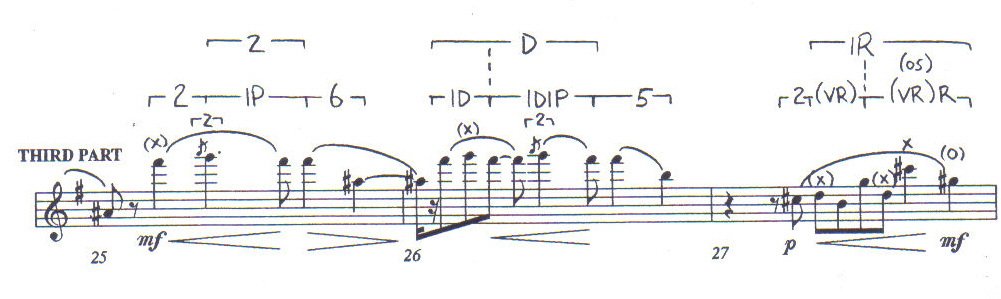
Example 1: Piano Concerto, first
Movement, measures 19-28, Piu mosso,
q = 96.
"Plano Concerto" by Samuel Barber copyright 1962 (Renewed) by G. Schirmer, Inc.
Example 2: Middle-level analysis
This phrase syncopates on a lower rhythmic
level as well. Note the [bl a b2 a] that
groups the falling arpeggios into three eighths. This conflict between motive
and meter and the ensuing deformation of the congruence between structural
tones and meter are aesthetically pleasing for their unpredictability and
freshness. The motive/meter conflict continues through measures 21 and 22,
disappears in the second part of the melody mm. 23-24), then reappears briefly
in the third and final part (mm. 25-27). In this respect, and in many others to
be discussed below, the three parts are dissimilar.
This comparison illustrates the
compositional plan of the theme: the gradual abatement of complexity. Both low
and high level structures and registral
differentiation underscore the disparity between the three parts of this
melody. Note that the first part consists of a four-bar phrase (or two two-bar subphrases connected by an underlapping
a1b a1 ..., the second part is a two-bar phrase united
by an upper-level process [P]; the final part contains three short one-bar
phrases unconnected on the high level. Thus the phrases grow progressively
shorter and more independent.
On the low level, Barber's strategy in
handling complexity is different. The opening string (mm. 19-20), P-RP(VR)-7, indicates that intricacy lies in the middle of the
phrase. The simplicity of the opening process [P] and the closing dyad [7] is
integral. These structures facilitate the motion into and out of the chain [RP(VR)], by initiating and terminating the underlapping a b a bl
a b2 structure. In fact, the high B is also the initial and terminal
note of the high-level I. ID (another a b a, see again
Example 2), join the three lower-level structures on a single higher level.
Thus the B that initiates the opening process and the B that initiates the
closing dyad anchor the first phrase.
The same pitch, B, becomes the point of
departure for the second phrase. As in the first phrase, this structure -
[embedded VP-P]-7 - is simple in the beginning and end, and complex (i.e.
multi-leveled) in the middle. The dyad [7] is marked with (i,
os) because: 1) the B is the resolution of the
dissonant A# , 2) it duplicates the structure Barber uses to close the previous
phrase, and 3) it is the completion of an underlapping
process that spans measures 19-22 (D# D C# C B).6
The subtle
difference between the descending resolutions of the dyads [7] illustrates the
aesthetically affective conflict between embodied yet suppressed low-level
implication and larger-scale patterning on the high level. The dyad [7] in
measure 20 is stylistically prospective, thus of little surprise, because of
the a b a ... patterning which "teaches" the listener to expect descent
from the B. In contrast, the dyad [7] in measure 22 is both prospective and
retrospective. As the terminal pitch in a registral
process [VP] initiated by D# and A# on the highest level, the B is prospective in
terms of registral direction and partially prospective
in terms of intervallic size. The denial of interval - large instead of small
- is made partially prospective by the underlapping
process from measure 19 that implies the specific pitch, B, as well as its
register.
The conflicting retrospective nature of the downward resolution of the dyad in measure 22 arises because of low-level interference with the high level. The ascending process on the quarter-note level, C F A, in measure 22 embodies ascent and implies a small interval, specifically, a minor second up to B, because of the harmony. This low-level implication, the ascent to B, persuasively fights those of the high level, descent to B, caused by the above mentioned registral process [VP] on the high level and the underlapping a b a... both in measures 19-23 and in measures 21-22. Thus the registral process [VP] is marked with a symbol (e) that indicates the conflicting presence of low-level embodiment. Had the A# in measure 22 resolved upward to B, the transformational tones, D , A, B, would have formed a reversal [R] with conflicting prospective (low level) and retrospective (high level) qualities.7
The second
part of this melody (mm. 23-24), while simpler than the first in many ways,
also displays hierarchical conflict.8 In measures 23-4, the low
level interferes with the middle level causing the middle-level registral reversals [VR] to seem prospective, rather than
retrospective. The ascent embodied in the low-level process [P, C# E# B, in
measures 2- 4 makes the first of the two middle-level registral
reversals [VR], G C#j B, prospective. The registral
and intervallic differentiation (A + B)
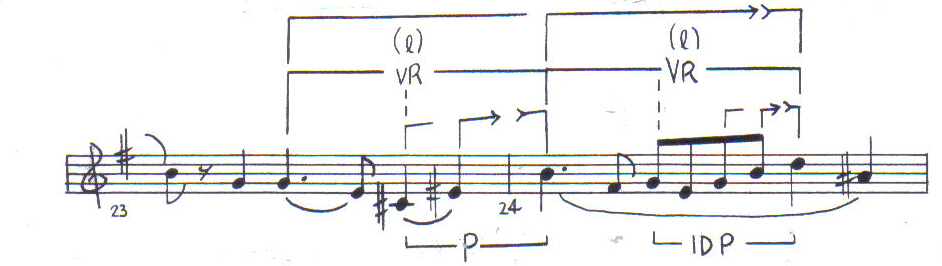
![]()
Example 3: Low-level interference
In contrast, the initial interval of the
second middle-level registral reversal [VR] (m. 24),
B G D, is smaller, a major third; thus the registral
reversal is less expected, all things being equal. However, all things are not
equal here. For the ascent embodied in the low-level process [P], E G B D, of
the IDP combination influences the upper level. In effect, the descent implied
in beats one and two on the middle level is challenged and overthrown by the
low-level ascending process in the second half of beat two. The low level makes
the change of direction (down - up) and the intervallic differentiation
(small-large) in the middle level [VR] prospective. Also, the first two notes
of the high level process [P, G B D, imply similarity of interval (small-small)
and register (up-up), enhancing the prospective nature of the registral reversal [VR] on the second level at the arrival
of the D in measure 24. Thus the interference from both high and low levels
virtually drains the aesthetic power of surprise from these usually highly
implicative and open structures.
A cursory glance at the structural symbols
of the third part of this melody (mm. 25-7) will reveal its simplicity relative
to the two preceeding parts. Note that there are
fewer levels, predominantly small (less implicative) intervals, repeated
intervals and pitches, and shorter, less dynamic phrases. We see, then, that
Barber's basic compositional plan is one of complexity moving toward
simplicity. Let us now focus our attention on the subtler hierarchical
conflicts that arise from relatively simple melodies constructed of fewer and
smaller intervals.
Violin Concerto (1940), Second Movement, measures 3-14
The conformance of the intervals, rhythms,
harmonies, and phrasing in this melody create an easily recognizable coherence.
Example 4) Unlike the raw energy of the fragmented
main theme of the first movement of the Piano Concerto, this melody gathers its aesthetic power from motivic
variation. The lower level consists primarily of four-note PIP structures
(eight of the sixteen structures are PIP) in which the IP, with one exception,
always moves from larger intervals to smaller intervals, or motion-left. Thus,
the most common structure of this melody is closural,
and not strongly implicative.
That such simplicity and conformity yield an interesting melody is remarkable. The subtle alterations these PIP structures give this melody its distinct, attractive profile. The richness of this motivic variation is manifest in the hierarchical conflicts between the low and high level, as well as in the changes in low-level structures from those implied to those that are unexpected.
Barber's subtle variation technique is best displayed in his handling of the two dyads [7] which are placed in the middle of the first and third phrases (mm. 3-4 and 8-9). Although the G# in measure 3 is the consonant tone of the two that create the dyad [2], the mildly dissonant [(x)] A transforms to the next level because it has a cumulation of 1:3 over the G . This affective G# A dyad is implicative, marked with (i), because the listener expects the beautifully suspended A, an upper neighbor note, to fall to the G# once it becomes clear that it is not going to ascend to B, (i.e. after two beats of the A).
The dyad in measures 8-9 is analogous, motivically, but the dissonance and consonance are reversed. Here, the initial note of the dyad, B, is dissonant and articulative, while the second note, C#, is consonant and transformational. This dyad is also implicative. The listener expects the CO to fall to B because of intraopus style [(os)] (i.e. since the tone following the dyad [2] in m. 4, G# tt, descends from A, the listener expects the same treatment here.) However, the dyad [2] in measures 8-9, B C#, does not immediately imply a downward resolution, as did the dyad in measure 4, because the C# is initially consonant with the harmony. Thus there is a conflict between intraopus style (implied descent) and bottom-up constants (implied ascent). However, with the harmonic change in measure 9, the C# becomes a suspension and the listener expects it to resolve downward, 6-5, to B. Note that the harmonic rhythm in the second half of this melody is faster than that of measures 3-7. The harmonic change on the downbeat of measure 9 gives the C new meaning. Had the harmony been repeated over the bar line, as it was in measure 4, the consonant C# would have seemed lifeless.9

Example 4: Violin Concerto, Second Movement, measures 3-14, Andante, = 84
"Violin
Concerto" by Samuel Barber copyright 1942, 1949
(Renewed) International copyright secured. All rights
reserved. Reproduced by permission.
Although many motives share the same analytic structure
[PIP], they are often functionally dissimilar given their particular contexts.
The first phrase, PIP-2-PIP-PIP (mm. 3-5), has a simple, familiar shape. It
rises serenely, accumulates tension with the open, implicative dyad, then falls
to closure. Note, however, that the final PIP is different from those that
precede it. It is more strongly closural,
motion-left, because 1) it descends and 2) the initial interval of the process
is a minor third, rather than a second. That is, the last PIP (mm. 4-5) moves closurally throughout, from larger intervals to smaller
intervals (m3 M2 u).
The second
phrase (mm. 5-7) resembles the first structurally, PIP-IP-PIP, and motivically in that the opening PIP of the second phrase
(m. 5, beat 4) is a transposition of the closing PIP of the first (m. 4, beat
4) (Example 5). An important difference between these two superficially similar
PIP structures is that the first is more closural
because it ends on a consonance with a change in harmony and because it is
placed at the end of the phrase. In contrast, the PIP initiating the second
phrase ends on a weak dissonance with no change in harmony over the barline. Thus, though these two motives are structurally
identical, they are functionally dissimilar.

Example 5: Identical structure, dissimilar function
Generally, the first and second phrases are similar. Both are more open in the middle of the phrase. In the second phrase, the first PIP (E C B B, motion-left, larger to smaller intervals) is followed by the rising IP (B A C , motion-right, smaller to larger Intervals) that is rhythmically open (quarter note, quarter note, half note). This IP is somewhat analagous to the dyad in the first phrase for its qualities of openness. With the exception of the tied CO that initiates the structure, the closing PIP (CO AGO, motion-left) of the second phrase is identical to the closing structure of the first phrase. Such similarities between the first two phrases make the small differences more effective.
With the exception of the treatment of the dyad (discussed above) and the PID (very similar to the PIP), the third phrase (mm. 8-1 0) is structurally very similar to the first. The variations that account for the new treatment of the dyad and the need for the PID rather than the PIP are the changes in scale degree in the melody and the harmonization. Whereas the first phrase rises from the stable tonic scale degree over a tonic harmony, the third ascends poignantly from the mediant scale degree supported by darker submediant harmony.
The PIPs that terminate the third phrase and initiate the fourth phrase recall
tleh motivic link between the first and second phrases. However, the two
PIPstructures are, in both cases, only superficially alike. In the latter
case, the second PIP (mm. 10-11) begins with a long note (four beats) and
moves, at first, toward closure, motion-left (B GO Fti)
like the PIP in measures 9-10. Then, however, it becomes more open, moving
motion-right (G# F# A).
The only chain [R(R)IP]
of this melody follows (mm. 11-12).10 On the low-level, the largely
stepwise, intervallically conformant melody gradually
shifts from small intervals to a mixture of small and large intervals. In the
stylistic context of this melody, fourths and fifths are large intervals;
seconds and thirds are small. Thus, Barber saves the larger intervals, which
initiate the fresh, contrasting reversal structures, for the final phrases of
the melody, measures 11-14. This, too, reveals Barber's strategy of altering
the patterns set up over the course of the melody. Also note that in measure 12
we hear the only articulative retardation on the
downbeat of a measure. The F# is a particularly
"good" note because all three previous phrases end on a consonance.11
The R(R) portion of the chain (A D# F# F#, mm. 11-12) is closural as it moves motion-left, circling in on, and
anticipating, the dissonant F# . The
dissonance resolves in the final structure of the chain, IP (F# F# G#). Had the F# fallen to E, as the listener might
expect it to, the phrase would have closed more decisively. The resolution up
to G# is mildly surprising. It keeps the IP more
open and implicative, and prepares the relatively large leap into the following
reversal.
The final PID-(VR)(R)
combinations over the subdominant-dominant progression (mm. 13-14) imitate a
stock cadential patterrn.
The high level influences the final reversal structure, making it seem
partially retrospective. The structural tones in measure 13 are C# above the
subdominant and D# above the dominant. Naturally, the listener expects E to
follow over the tonic. This would create the analysis (VR) (IP). However Barber closes melodically on B, thus creating a reversal
that is neither prospective nor retropective because
the B is anticipated. The 'celli play the anticipated E an octave lower
as they take the melodic line. Thus the phrases dovetail elegantly.
If the
listener hears measures 10-14 as a single extended phrase, as I do, then the
formal relationship of the four phrases should be identified as A (mm. 3-5) B
(mm. 5-7) A1 (mm. 8-10) C (mm. 10-14). This formal organization is
readily apparent in the structures formed on the second level. Remember that
the second level IPP

Example 6: Second-level analysis
Also displayed in the high level analysis are the level interferences that subtly add to the aesthetic affect of this deceptively simple melody. One change of direction occurs in the high-level IPP structure of the first phrase. Relative to the first, the second structure, (R)VR, which changes direction twice, is more closural. Although the first change in registral direction is unexpected, (R)], the second, [VF1], is expected. Thus, the usually prospective reversal structure and the usually retrospective registral reversal structure are altered by low-level interference (Example 7). The reversal is influenced by the low-level intervallic process [IP] because the denial of register, B A C#, is unexpected. Note that this is the first motion-right structure in the melody. Thus, the implied high-level process, E B C#, reverses unexpectedly. The usually retrospective C# A G#, of the PIP on the low level implies descent. Such dynamic interaction between levels denies the listener the expected high-level structural tones while providing the comforting familiarity of the low level structures (i.e. the PIPs).

Example 7: Low-level interference
As I mentioned above, the high-level RP structure of the
third phrase (Example 6) is very much like the IPP of the first. These similar
structures reveal the formal similarities between the phrases while indicating
that there is a fundamental difference between them. The difference stems from
low-level variation. The ID half of the low-level PID combination (m. 9),
denies registral direction by ascending and returning
to B. On the high level this creates a reversal [R], G# C# B, rather than, say,
an intervallic duplication, G # C# G#i or G# C# A, an intervallic process.
A look at the high-level symbols of measures 10-13, the
first half of the final phrase, might indicate that this phrase is highly open.
Yet the PVP, which spans a seventh, B C#, is largely the result of the
necessary melodic return from the dominant scale degree to the closure of the
final cadence. In fact, the closural structures on
the lower level (i.e. reversals) conflict with the openness of the upper
One final observation, on the parameter of
meter, supports the argument that the key to this melody's aesthetic effect
lies in subtle variation. The ambiguous nature of the meter in the opening
measures (i.e., the variation between six-four and three-two)
brought out by the interplay between horns and first violins allows the melody
to seemingly float, within a flexible meter, through the first measure. In
fact, the opening ascent to A can be parsed in two ways, one in each meter.
Though the violins eventually clarify the meter in measure 4, the same
flexibility can be heard again in measure 8. These moments of metric ambiguity
breathe life into this melody.
The subtle variation techniques that
individuate the delicate phrases of the slow movement of the Violin Concerto
are also found in the slow movement of the Piano Concerto. The two
melodies are alike in that they both are deceptively simple, constructed of few
motives and highly similar phrases. The latter is, however, somewhat more
complex, because it is not rhythmically homogeneous, as is the former, nor do
the phrases resemble each other as closely .
Piano
Concerto, Second Movement, measures 1-9.
The immediately apparent formal repetition of phrases is, in the Piano
Concerto as it was in the Violin Concerto, deceptively simple. This
melody plays with the listener's expectations of formal repetition because
Barber's strategy centers on the modification of intraopus
style structures. Although high-level structures indicate the readily apparent
similarities between phrases (e.g. measures 2 and 3, 4 and 8, 6 and 7, see
Example 8), close inspection of the low levels of this melody supports the idea
that such formal relationships between phrases can be reductive. The aesthetic
pleasure derived from the subtle variations from phrase to phrase can be best
understood from the low-level structures.
Each phrase borrows and/or alters some aspect
of the phrase it follows. The phrases can be labeled as A-A1-AB-B1-1-
BA. Each letter or pair of letters accounts for one of the six phrases. The
meaning of these symbols will become clearer after a detailed discussion of
each phrase. The second phrase (m. 3) is much like the first (m. 2), but the
closing dyad is deformed to create a dependant relationship between the second
and third phrases. The third phrase (m.4-5) is similar to the first and second
in rhythm and the use of the dyadic beginning and ending. Its ending more
closely resembles that of the first phrase because the dissonance resolves. As
a result of the altered treatment of the opening dyad, the third phrase has an
entirely new high-level structure, P. The fourth phrase (m. 5-6) grows out of
the new melodic shape in the middle of the third phrase and maintains the use
of dyadic beginnings and endings. The fifth phrase (m. 7) subtly varies the
fourth. Finally, the sixth phrase (mm. 8-9)

Example 8: Piano Concerto, Second Movement, measures 2-9, Moderato, q = 44
"Violin Concerto" by Samuel Barber copyright 1942, 1949 (Renewed) International copyright secured. All rights reserved. Reproduced by permission.

Example 9: Second-level analysis
The first phrase, 3-ID-ID - P-2, moves
from simplicity, the dyad [3], to slight complexity, dyad [2] (see again
Example 8). The opening dyad, E C#, is the germinal
cell of this melody, as it is at first integral to the two embedded processes [P], and then initiates the low-level process (C# E G#). The G# transform. and becomes a structural
dissonance because of its strong metric position and cumulation.
It implies F a harmonically weak resolution. Thus the dyad is implicative and
is marked with an (h). The G# is a particularly
"good" note because intraopus style (os) and harmony make the F#,
instead of the G , the expected note. The leap (E G#) to a cumulative moderate dissonance [x] on a strong beat
is affective.
Note Barber's consistent use of dyadic
structures to open and close the phrases of this melody. The opening dyads do
not function, like many opening dyads, as anacruses.
The treatment of the dissonance, consonance, duration, and transformational
power of both opening and closing dyads changes throughout this melody. Such
subtle variation in dissonance, consonance, and hierarchy in the repetition of
these structures adds to the delicacy of this melody.
For example, although the symbols on the
low level of the second phrase, 3-ID-ID-P-2, duplicate those of the first
phrase, marked differences exist between the meanings of these symbols. Both
opening and closing dyads of the second phrase (m. 3) are treated differently
from those of the first phrase (m. 2) with regards to dissonance and transformation.
In the case of the opening dyad [3] in measure 3 the initial note is a weak
dissonance, [(x)]. In measure 2, both notes of the opening dyad [3] are chord
tones. In the case of the closing dyad in measure 3, both notes are
The D# and the contramodal
C in measure 3 are strongly implicative. They deny the closure implied by intraopus style learning in measure 2 where the dissonant
[x] first note (G#) of the dyad [2] resolves to the second note (F#). The
dissonances in measure 3 differ because they require further resolution. This
conflict between melody and harmony is shown with the (h) above the dyad [2].
The expected resolution of the D# comes in the oboe's initial E (m. 4). Thus
the variation in the treatment of the closing dyad in measure 3 joins measures
3 and 4 on the low level, shown by the horizontal dotted line. This linkage
between phrases two and three (mm. 3-4) is unexepected
because phrases one and two (mm. 2-3) are separate on the low level. The a b a1 D# C E, and the steady crescendo through the end of the
flute phrase also helps dovetail phrases two and three.
The third phrase offers yet another
treatment of the dissonance, consonance and transformation of the pair of
dyadic structures. At first, the new twist seems to be the metric displacement
of the first dyad. But that is only part of the scheme. The interval of this
dyad is a second [2], rather than a third [3], and in this case the first note
(E) is consonant while the second (DO) is a weak dissonance [(x)], which yields
the opposite placement of the dissonance in the opal... .g
dyad in the preceding phrase (m.3). Also the second note is counter-cumulative
in this measure, whereas it is cumulative in the first two. These variations
affect the high-level structure as well as the low-level perception of this
phrase. Note that it is the initial note of the dyad in this phrase that
transforms to the second level. This is not the case in the
first two measures.12
In the third
phrase (mm. 4-5) the melody adds new structures to alterations of the familiar
ones discussed above. From intraopus style (os) learning we might expect in measure 4 an intervallic
duplication to follow the opening dyad. The harmonic change to an augmented
chord B# E G# on beat three strengthens this
expectation. The first IP (D# G E) of the IPPIP chain is marked with (h)
because the harmony leads the listener to expect the change in registral direction and perhaps even the specific pitch, E,
as the resolution of the D#. The a b al and the x (!)
(o) highlight this relationship. The leap up to the G#, not the nearest resolution of the DO, but a chord tone
nonetheless, is a small surprise. The ensuing chain, IPPIP, is a welcome change
because it introduces a new structure to the meiody.13
Closure is strengthened by strong
motion-left through the ensuing IP-2. This symbol (mL)
indicates the propulsion of the melody toward G. The initial note (A) of the
dyad [2] is a "good" note because the Fx
embodies reversal to G# . Thus
the dyad [2] is marked with (h). Barber delays the implied resolution with a
cumulative dissonance, A, much as he did at the end of the first phrase. Note
the further similarity between this phrase and the first. They begin simply,
with dyads, move toward complexity (embedded structures), and end simply, with
implicative dyads.
Further transformation of this melody
leads off the fourth phrase, IR [embedded PIP-IP]ID-2
(mm. 5-6). The embedded PIP-IP (m. 5, beats 3 and 4) imitates the chain of the
previous phrase (IPPIP, m. 4) and functions as an upbeat to the passage with
the most embedded melodic structures (m. 6).14 The complex embedding
in measure 6, which resembles an augmented turn, results from various
influences of harmony and voice leading. The B, a lower neighbor note to C, is
dissonant against the A in the harp and violins. The E is dissonant against the
F in the accompaniment. Barber uses a dyad [2] to reach closure. Note that this
dyad differs from those that come before in that it has an embedded trill.
A subtle variation on the complex chain in measure 6 follows in measure 7. The IP structure embedded under the IP in measure 7 is an aesthetically pleasing surprise because the large leap up to G# is unexpected, particularly due to this phrase's similarity with measure 6. The closural dyad is implicative, a resolution from a half-diminished seventh chord to a fully-diminished seventh. This is made clear by the flat trill. In contrast, either C or B can be considered a chord tone in measure 6. From intraopus style learning, the listener might hear the former as an appoggiatura.
Measure 8, the sixth and final phrase, combines phrases two and three (mm. 3-4) motivically. The underlapping dyad, [2] rather than [3], resembles measure 4. The dissonance and the lack of syncopation of the initial note of the opening dyad and the embedded processes [P] and intervallic duplications [ID] recall measure 3.
It is interesting to note the conflicting degrees of closure from level to level. The final phrase closes with non-motion on the low level, motion-left on the middle level, and motion-right on the higher level. The closing low-level intervallic duplication [(ID)] (mm.9) is retrospective because of intraopus style interference. That is, because the closing low-level structures in measures 2-7 are all dyads, the intervallic duplication in the final phrase is at first, unexpected, and thus retrospectively closural.
It may be helpful to restate the motivic relationships between phrases described previously as A-A1-AB-B-B1-BA. The second phrase (m. 3) is much like the first (m. 2), but the closing dyad is deformed to create a dependent relationship between the second and third phrases. The third phrase (mm. 4-5) is similar to the first and second in rhythm and the use of the dyadic beginning and ending. Its ending more closely resembles that of the first phrase because the dissonance resolves. As a result of the altered treatment of the opening dyad, the third phrase has an entirely new high-level structure, P. The fourth phrase (m. 5-6) grows out of the new melodic shape in the middle of the third phrase and maintains the use of dyadic beginnings and endings. The fifth phrase (m. 7) subtly varies the fourth. Finally, the sixth phrase (mm. 8-9) recalls the second and third, combining their materials into a new structure.
Violin Concerto, First
Movement, measures 1-11
Deceptively simple, this melody is, perhaps, the most Elegant of the
four discussed in this critical study (Example 10). Its sub-phrases are woven
into an extraordinarily seamless eleven-bar phrase. The key to this melody's
beautiful sense of forward propulsion lies in the interlocking of denied,
abandoned, and/or deformed implications in the measure-to-measure level
structures which finally blossom (i.e., realization is achieved) when the high
B is reached in measure 8. This having been said, the low-level structures will
not be given quite the same exhaustive treatment as have those in the previous
analyses. Still, it is necessary to address issues of smaller importance first
to lay some of the groundwork for the closing
discussion.
One of the problems encountered in analyzing this melody is
that the nature of dissonance and consonance varies from measure to measure.
This has a direct effect on how the melody is parsed. For example, the A in
measure 2 is a mild dissonance [(x)] in a downward enveloping process (E C A
F0). Thus the melody does not break on that A. However, in measure 4, A is a
chord-tone dissonance because the horns sustain the seventh and the eleventh
above the root, blurring the subdominant. For this reason, and due to the
influence of intraopus style learning from measure 3,
the melody breaks on the A, and parsing occurs on the eighth-note level in
measure 4. Such distinctions are important because they directly influence .one
dynamics and meanings of the analytic symbols.
Intraopus style further effects the low-level parsing of this melody in
measure 5. With the subdominant harmony, the D on beat two is mildly
dissonant [(x)]. It subsequently resolves to C. Therefore, ;t
seems the dissonant note (D) should be enveloped in a combination. However,
this D occupies the metric position of an important implied structural tone,
namely C, due to an intraopus style pattern found on
the second beats of measures 3 and 4, A (D) C. Thus, this measure-to-measure
patterning, along with the effect of cumulation,
causes the melody to break on the mildly dissonant D.
Barber's interest in subtle motivic variation is as amply displayed in this melody as
it is in the slow movements of his piano and violin concerti. For example,
measures 3 and 4 are very much alike formally, but the analytical symbols
reflect their subtle dissimilarities. Measure 3 is constructed
of two separate structures, P and IP, on the low level. They are not linked
because of the cumulation on A
(beat 2) and the stress on the first note of the three-note upbeat to measure
4. The triplet figure helps separate the two structures (P and IP). In
contrast, the augmentation of the analogous three-note upbeat figure in measure
4 stresses the second note (A), thus breaking the melody on beat four of that
measure. This creates three adjacent structures, P-IP-IP, that flow smoothly
from one to another because they link on the low-level.
Another example of motivic
variation in measures 8-10 helps abate the climactic tension through formal
repetition of the descending thirds figure of measure 2 (see again Example 10).
These echoes of melody break into smaller chunks, beat by beat, because they
lack dissonance. In this manner, they become more closural
and less implicative, which seems fitting as they are essentially cadential. Even so, Barber makes this figure elastic, and
therefore interesting, by recycling the different groupings of the same notes
through a repetitive rhythmic pattern. For example, the triplet figure changes
from an intervallic process [IP] in measures 9 and 10 to a combination [PIP] in
measure 10.
The leap up a tenth to D (m. 10) also
derives its beauty from subtle variation. After numerous repetitions of the
descending arpeggio pattern (mm. 8-10) followed by an upward octave leap, to B,
the leap from B to D is fresh and pleasantly surprising. Although this melodic
fragment's structure [VR] is, at first, highly open D B D1, it is
immediately followed by a strongly closural reversal,
B D1 D1. The closure of the
reversal [R] is, however, exquisitely suppressed by
the dovetailed arrival of the opening melody, supported by a seventh chord in
third inversion. Thus as the melody closes, the harmony becomes implicative.
Similar to the compositional plans of previously discussed melodies, the middle-level symbols indicate patterns of simplicity moving toward some of considerable complexity, followed by a return to simplicity. For instance, complexity begins in measure 3, where the reversal [(R)] of the IP(R) structure seems retrospective because the listener expects the Ft on beat 4 to resolve upward to G when the subdominant arrives in measure 4. However, the F# is reiterated and becomes part of the chord, C 13, and therefore a structural tone on the next level.

Example 10: Violin Concerto, First Movement,
measures 1-11, Allegro, q = 100.
Also, that nearly identical phrases generate
different middle-level structures (e.g. [RP] in measure 4 differs from IP(R) in
measure 3, a phrase that is nearly identical)

Example
11: Nearly-identical
phrases with different middle-level structures
Another element that enriches this melody is
the conflict of registral direction implications
between levels. For example, the tendency of this melody to descend in the
middle level is sometimes counteracted by the insistent rise of the low level
(Example 2.) The leap up to G on the last eighth-note of measure 5 is
particularly beautiful due to the conflict between levels. The middle-level registral reversal [VR], D C G, in measure 5 is partially
retrospective because the falling D C of the reversal (R) on the middle level
implies a continuation of registral direction, downward, and similarly of interval, small. This conflict between
levels makes the large leap up, initiating the reversal structure that leads
into measure 6, a pleasant surprise.

Example 12: Conflict of registral
direction between levels
The inter-level conflict between
rising and falling is apparent in the next phrase as well. While the middle
level G F# implies registral
continuanward, the low-level process
F# G
implies ascent. The down-up pattern on the middle level is also influenced by
the intraopus style of motion doweasure 5. Thus the low-level
changes of down-lateral registral direction is
expected in the intervallic process [IP], marked (os),
and the middle-level intervallic process [IP] is also somewhat prospective,
marked ("I") (see again Example 2.)
Interestingly
enough, the tendency of the second level to descend in measures 3-7 conflicts
with the third level's implied ascent (Example 13). The descending registral direction is implied then denied, on the
syncopated half-note level. At the same time, two ascending processes are
realized on the whole-note level.
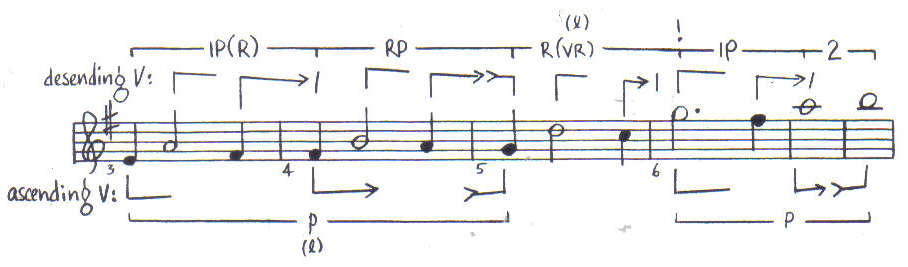
Example
13: Inter-level conflict
There is, finally, an aspect of this melody that is as
equally important in providing the listener with an understanding of its
extension into a seamless eleven-bar phrase as the previous discussion of
subtle phrase variations and level conflicts. As I stated above, the key to
this melody's beautiful forward propulsion lies in the interlocking of denied,
abandoned, and/or deformed implications in the measure-tomeasure
level structures which finally blossom (i.e., realization is achieved) when the
high B is reached in measure 8. To explicate such a hypothesis, it is necessary
to lay out the various underlapping processes and
their implications.
Example 14 illustrates the numerous implicative patterns.
The realized process on the whole note level, E F# G, emerges both
retrospectively and prospectively. This retrospection is due to the influence
of the implied registral descent on the second level.
The medial note of the high-level process, F# is not implied on the middle
level because the retrospective reversal [(R)], part of an IP(R) combination,
denies registral continuation downward. On the other
hand, the terminal note of the high-level process, G, is implied by the
middle-level process that is combined with a reversal.
![]()
![]()

Example
14: Numerous implicative
patterns
Simultaneous with the high-level process is an a b al b1 a2 b2
The underlapping dyads [4] in measures 3-4 are the combination
of the a and b of the a b a1... pattern (Example 15). This motive, initiated by the
sixteenth notes on the lowest embedded level, implies continuation in measure
5. However, the pattern is broken by the arrival of a new rhythmic and
intervallic structure, the dyadic fifth, shown underlapping
the reversal on the downbeat of measure 5. Even as Barber denies the processive implication of the dyadic fourth motive, he initiates a new one, for another dyadic fifth motive arrives
on the fourth beat of measure 5. This, in turn implies another motivic process. The reversals [IR] in measure 5 (beats 1
and 4) introduce a new structure and larger intervals. The following pair of
structures, IP- P

Example 15: Underlappng dyads

Example 16: Complex conflict between levels:
the approach to the climax of the phrase
The lack of congruence between parameters
at the climax of the phrase in measure 8 is particularly noteworthy. First, the dynamics diminuendo from forte on the A in measure 7 to
piano on the climactic B. Second, the B is durationally
counter-cumulative, an eighth note, relative to the initial and medial notes of
the high-level process. Third, the bright upper register is immediately
abandoned in the octave descent to the low B. Finally, the tempo resumes
immediately, advising the soloist and conductor to press on at the highpoint.
Such understatement renders an exquisite climax.
The aesthetic affect of the non-congruence
between separate parameters at the climax discussed above is analogous to the
power of non-congruence between hierarchical levels of analysis. The richness
of these melodies, and all melodies, is, in part, derived from such cognitive
conflicts between embodiment of suppressed implication from the low-level and
large-scale patterning on a high level.
1 For a thorough discussion of this theory, see Eugene Narmour, The Analysis
and Cognition of Melodic Complexity. Chicago: University of Chicago Press,
1992.
2 Keep in mind that implications and realizations take place on many levels. The interaction of levels either reinforces or interferes with our on-going understanding of the melody.
3 The variables in the
formulas (A,B,C) can stand for both small-scale and
large-scale elements in music. They apply to single elements in a parameter,
such as a pitch or an isolated duration, and to relationships within a
parameter, such as interval (I), registral direction
(V), or rhythmic patterns, as well as to form on any level.
4 Consequently, their ability to manifest the strength and depth of Eugene Narmour's implication-realization theory of melody.
5 Ascending and descending processes
EP] tend to envelop additive and counter-cumulative rhythmic relationships,
regardless of metric accent. Thus, I do not parse the melody on the downbeat of
measure 20 because the G is the medial tone of a metrically enveloping process
(B G D), which is the middle structure in the RP(VR)
chain.
6 The second half of this underlapping process is marked with a dashed line because
the C comes so much later than the C#. While this descending process might not
be immediately apparent, I believe the formal similarity of the closing dyads
makes it noticeable. Also, this helps account for the resolution of the A# to
the B a major seventh below. That this resolution is an octave lower than
expected makes the B a particularly "good" note.)
7 Not only does the
hierarchical conflict of the dyad [7] provide the listener with a rich
aesthetic experience, it also makes apparent one of Barber's most effective
compositional strategies: the inventive and unconventional use of the dyad.
Dyads as anacruses can be found in almost all of the
musical literature, for the notion of upbeat-downbeat is widespread. However,
the use of the dyad as a closural structure also
became somewhat of a cliché in tonal western music, when aesthetically
pleasing appoggiaturas became cadential style
structures. As we can see in this melody, Barber took this style structure and
"modernized" it, for the closural dyads
here are of such large intervals that they hardly resemble those of, say, the
eighteenth and nineteenth centuries. Yet they function in much the same way.
The second movement of this concerto makes this clear, for the dyads are
smaller, seconds and thirds, and seemingly much more conventional. This is not
to say that all of Barber's closural dyads are either
conventional or modernized conventional style structures of the eighteenth and
nineteenth centuries. The dyads in measures 20 and 24-26 imitate that style structure,
but do not have the resolution from dissonance to consonance necessary to make
them function as such. Thus, a third kind of closural
dyad is that of stylistic imitation.
8 The relative simplicity of these measures lies in the use of
smaller intervals, lack of syncopation, the predominance of low and high-level
realization. The low-level structures, l-DP-(R)-IDP-4, and the highest level
structure, P, indicate the prevalence of realizations.
9 Because the second tone
of the dyad in measure 3 is dissonant, the listener may initially perceive the
second tone of the dyad in measure 8, C#, to be dissonant as well. That this
tone does eventually become dissonant is somehow pleasing. Barber has his cake
(i.e., the illusionary, intraopus style-influenced,
implicative dyad in m. 8) and eats it too (i.e., the actual implicativeness
of the dyad at measure 9). Such subtle variation in the treatment of dissonance
in this melody is truly elegant, for it not only affects the low-level
structures, but also alters the implications on the higher level, to be
discussed later.)
10
Unlike the
compositional plan of the first movement of the Piano Concerto, that of
the second movement of the Violin Concerto positions the most complex
phrase at the end. The reversal structures on the lower level seem well-suited
to this final phrase (mm. 10-14) for they are more closural
than the IPs which end the first three phrases.
11 The F# in measure 12 occurs over a change of harmony. This makes it stronger than the B in measure 6, where the harmony does not change.)
12 Of the two
tones that form the opening dyad in the first, second, and sixth phrases, the
second is the structural tone. In all three instances, the second tone is
cumulative. In the second and sixth phrases, the first note of the dyad is
deformed, though by different degrees, by dissonance. Note again that it is the
initial note of the opening dyad of the third phrase (m. 4) that transforms. Of
the two tones that form the closing dyad in the first, third, fourth, and fifth
phrases, the second is the structural tone. The deformational dissonance on the
terminal note of the dyad in the second phrase (m. 3) prevents closure on both
high and low-levels. Thus, as I indicated earlier, Barber's varied treatment of
dissonance in the dyads on the low level alters the structural tones on the
upper hierarchical level. The high-level symbols reflect the subtle variations
from phrase to phrase.
13 The
addition to the chain structure in the third phrase is perhaps formally
expected as A + A --> B.
14 The IP embedded under the IR influences the latter structure
because the former implies a small interval in the opposite direction, namely
the resolution of the B to C. This makes the continuation of register and
differentiation of interval implicative on the upper level, B D C.