An Overview of Karel Janeček's Foundations of Modern Harmony
John MacKay
The central interest of this overview is in the content and coherence of Janeček's theories which, while similar in their systematic rigor to North American models, have pursued a more radically harmonic formalism as well as a certain more compositional (as opposed to analytical) orientation. In addition to the formidable scope of Janeček's thinking, we also see in the treatise its unique relationship to musical/stylistic and pedagogical issues, as well as the tenaciously empirical mind set with which Janeček approached the many theoretical and epistemological challenges of his work. Moreover, this latter factor of Janeček's empirical mind set, provides an interesting point of departure for this discussion as he reflects in his preface on his concept of the "absolute" nature of dissonance which had always been at the heart of his work:
For example, I consider the prevalent view about the shifting of the boundary between consonances and dissonances to be such an assumption. I have encountered this view in almost every interpretation of modern harmony, and I once supported it myself. I finally realized that with such a bias problems of harmony cannot be resolved honestly. It is precisely that rich diversity of existing dissonances that tempts theorists to think that chords once considered dissonant have now become consonant and that the range of consonances is thus expanding. Although I have studied dissonances thoroughly, I have never converted any of them to consonances. I realized that shifting the boundary between consonances and dissonances was tantamount to admitting that there is no substantial difference in sound between these two categories of chords. The superiority bestowed on consonances by nature would then be fictitious. (3)
Only by sketching a classification of chords according to their sonic character did I proceed to investigate all possible chords in the tempered chromatic system. I was led to this by the realization that theorists with whom I had become familiar were all working under the assumption that the possible chords were virtually unlimited. I studied this assumption, then generally tacitly accepted, and finally concluded that it was not true.
The consequences were far-reaching. It became apparent that it was possible to work out a classification of all chords according to character. From this detailed classification, boundaries between character types as well as the extent of individual chord groups could be clearly seen. The all-inclusive nature of the classification is demonstrated in this book, and I believe it to be a basic feature distinguishing the book from other treatises and theoretical systems.
Thus Janeček cites the "dissonant element", i.e. the traditionally conceived dissonant intervals plus the unique trichordal component of the augmented triad (a dissonance composed purely of consonances), as the starting point in his classification of harmonic material. Prior to this, however he lays a meticulous groundwork, classifying atonal harmonic materials along traditional lines of chord "disposition" (the registral placement of the elements of a chord) "chord-type" (chords related only by transposition and change in disposition) and the more abstract, and for its time, radical, "orientation scheme" which was a type of "root position" or "harmonic prime form" (but without inversional equivalence) as defined by the most compact disposition of a sonority with intervals stacked in increasing size from the lowest tone.
When Janeček turns to matters of motion and tonal function, in chapters six through nine (4) of the treatise he pursues principles defined by earlier Czech theorists, in particular Leos Janáček's "imaginary pitch" (5) and a revised Riemanian system of functional harmony which he adapted from his mentor Otakar Šín, to whom the entire Foundations is dedicated. Here he relies more on conjectural extensions of these existing frameworks than on his commitment to listening intuitions and classifications which govern his discussion of static chords. The closing chapters provide a synthesis for the work, elaborating an extensive variety of compositional and analytical applications and revealing much of the stylistic and compositional roots of his theoretical ideas.
In reducing the seemingly infinite universe of chords to transpositions, and re-dispositions of basic two-, three-, four-, up to twelve-note forms, Janeček develops his "orientation scheme" in the guise of an abstract root position. The trichord CGD (Example 1), for example, is compressed to its narrowest forms, GCD and CDG, with preference for the latter as the orientation scheme since its smallest interval (the C-D) is on the bottom of the structure. The numerical representation of the orientation scheme records only the intervals (in number of semitones) between the ascending tones of the structure, thus yielding 2 and 5 semitones (written "25") for the CDG trichord (Example 1a). To facilitate the listing of different dispositions and the representation of symmetrical structures which are not apparent in the orientation scheme, the octave "complement" (the interval which completes the octave) is added in brackets to the numerical representation, followed by the basic orientation scheme repeated thus giving an "expanded orientation scheme" of 25 (5) 25 once more for the CDG example. From this the different harmonic permutations can be read in the successive left-to-right groupings 55 and 52 (i.e. C-G-D, or G-C-D), the former of which (55) reveals the symmetrical nature of the structure.

Example 1: Calculation of Orientation Scheme 25 and Other Dispositions from "Expanded Orientation Scheme" 25 (5) 25
For each structure,
Janeček then configures the "harmonic scheme" to represent the most
"harmonic" disposition of an orientation scheme, projecting wherever possible major or
minor triads (43 and 34, i.e. stackings of major and minor thirds) and sevenths from the
lowest note. Any clusters (adjacent intervals 2 or 1) are broken up but the smaller ambit is
still preferred unless a larger ambit will show the symmetrical structure more clearly.
For example, the harmonic scheme of the chord 1313 (G#ACC#E) is given as
![]() which optimizes the number of major and minor triads indicated by (respectively)
square and round brackets with a star designating the lowest tone of the
orientation scheme. Unlike the orientation scheme, there may be several harmonic
schemes for a single chord.
which optimizes the number of major and minor triads indicated by (respectively)
square and round brackets with a star designating the lowest tone of the
orientation scheme. Unlike the orientation scheme, there may be several harmonic
schemes for a single chord.
In generating all possible three-note orientation schemes, Janeček crosses categories of symmetrical and asymmetrical chords with "traditional dissonant" and "traditional consonant" 3-note chords, as well as "new" dissonant 3-note chords, and "traditional incomplete 4-note chords". He then categorizes four- and five-note chords into "symmetrical" and "asymmetrical" which he cross-categorizes with "diatonic" and "chromatic", showing increasing membership, particularly in the five-note chords, in the "asymmetrical chromatic" category. In the tables, symmetrical chords are indicated with bi-directional (up and down) arrows, and single-direction (up or down) arrows, together with the long dashes, indicate pairs of non-symmetrical chords which are related via inversion (i.e. 43-34 etc. see Example 2 for representative excerpts of Janeček's tables of orientation schemes.)
3-note chords - symmetrical traditional new dissonant

- assymmetrical traditional consonant and new dissonant
incomplete 4-note chords 3-note chords
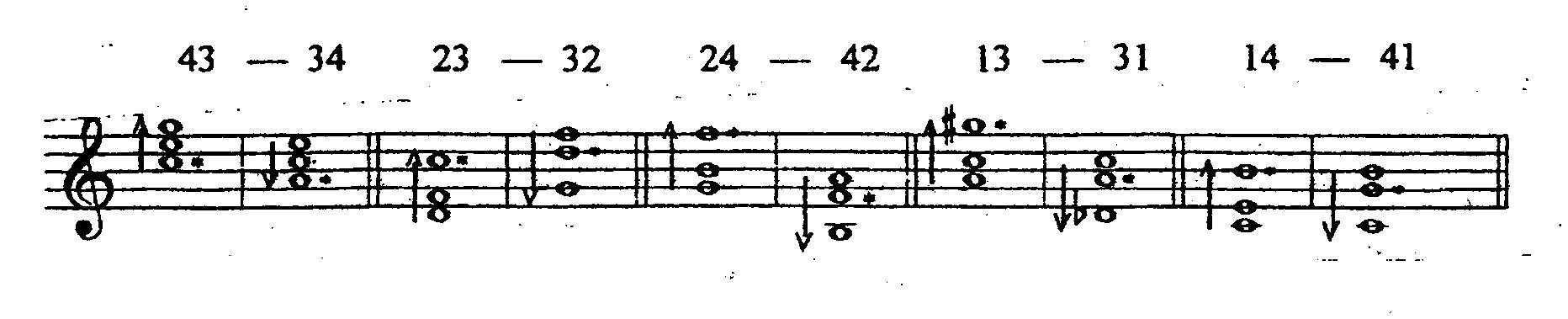
4-note chords
symmetrical diatonic chromatic

asymmetrical diatonic

chromatic

5-note chords
symmetrical diatonic chromatic

5-note chords
asymmetrical diatonic

chromatic

Example 2: Representative Excerpts from Janeček's Tables of Orientations Schemes for 3-, 4- and 5-Note Chords
With the introduction of the "negative", or the 12-tone complement of an orientation scheme, six-note chords are divided into the following groups: those whose negative has the same orientation scheme as the original (in both "symmetrical" and "asymmetrical" categories), those asymmetrical hexachords whose inversions are also "negatives" (12-tone complements) of the original, and those six-note chords whose negative is of a different type. In Janeček's examples the asymmetrical chords are similarly all arranged in inversionally related pairs (See Example 3).
Considerable elaboration ensues at this point on the derivation of orientation schemes of "multi-note" chords (i.e. chords of more than six notes) from the orientation scheme of their smaller "negatives" and other observations concern the unique properties of the diatonic scale (i.e. the diatonic 7-note orientation scheme) and the symmetrical 8-note structures of limited transpositions. The orientation schemes of particular diatonic collections are surveyed including the "pure diatonic", its negative, the pentatonic, the "melodic major" and "melodic minor" scales, the "gypsy minor" and "gypsy major", the whole-tone scale, and the isometrical "harmonic major" and harmonic minor scales. Observations of varying substance then focus on the membership of chords and their intervallic inversions within symmetrical and asymmetrical scalar systems and also on the use of the expanded orientation of a scale to find particular chord members.
Example 3: Representative Excerpts from Janeček's Hexachord Tables Consonance, "Dissonant Elements" and "Characteristic-Types"
Having established a viable analytical and notational framework, Janeček moves on to study consonance and dissonance and their role in an expanded chord classification. Accepting a fairly standard and subjective definition of dissonance as any "chord type that arouses a sense of unrest and tension in the listener under all conditions" (i.e. "in any disposition without regard to its place in a chord succession") he then attributes dissonance more specifically to the presence of one or more of the four "dissonant elements": the semitone (interval "1"), the whole tone ("2"), the tritone ("6") and the one three-tone element, the augmented triad which is designated either as "44" or more often as "0". Only chords not containing any of these elements are consonant; these are limited to the non-dissonant intervals (i.e. the 3rd, 4th, 5th, 6th etc. which Janeček calls "two-note chords") and the major and minor triads which are seen as the "richest possible consonant chords". Harmonic inversion is taken to have no effect on the fundamental consonance or dissonance of a single chord or chords related by intervallic inversion (i.e. the major and minor triads, the dominant and half-diminished sevenths, etc.).
Qualitative criteria further categorize the fundamental dissonant elements themselves. The semitone is seen as "obtrusively piercing" and "unusually noticeable, evoking acute tension", the whole tone as "insipid" (i.e. dull), "unobtrusive", causing a "certain blurring" and evoking" only mild tension". The tritone is, on the other hand, "mildly stimulating", exerting a "fusing effect" and a "coalescent impression" in chordal structures. Finally, the augmented triad is "noticeable without being piercing" - as a somewhat "warped" major triad its "characteristic flavor" can be easily recognized in more complex chords.
Janeček then builds a characterization of dissonant structures starting from the "single and unmixed" dissonances (i.e. chords which contain a single instance of a single dissonant element, see chart; Example 4) in which he distinguishes between "classical" and "modern" harmonies. The dependent and catalytic nature of the tritone is evidenced by the absence of any four-note chords that contain the single tritone as the only dissonant element. More ad hoc observations are made concerning the role of "full" consonances (thirds) and "open" consonances (fourths and fifths) in these structures, the former (in "a", "b" and "c" of the whole-tone series) having a greater "softening" effect on the dissonance than the latter ("d: in the same series)

Example 4: Janeček's Chords of Single Dissonance Characteristics
Janeček next considers structures containing a single dissonant element but which occurs more than once in the same structure. Thus in relation to the simple dissonance E-D#, the structure G#-E-D#-G (see Example 5) has an "increased" dissonance characteristic of the M7 (that of the simple interval of G#-G) which is nevertheless somewhat "softened" by the intervening consonances. The "increased" dissonance is distinguished from the combination of dissonances which produces new, "merged" dissonances such as in the major second arising in the superposition of M7s. (See Example 5c the D-C major second in the superimposed major sevenths D-C#-C.)

Example 5: Isolated M7, Increased Dissonance of M7 and Superimposed M7s with "Merged" M2
Thus there is only one "genuine" increase of the semitone dissonance (Example 6a) and whole-tone dissonances, as Janeček notes, can be stacked directly and indirectly by superimposing fourths, thus "increasing" the dissonance once and twice in the various 3-, 4- and 5-note sonorities of Example 6b. The tritone can only be "increased" by combination at the minor third yielding the diminished seventh chord (see Example 6c).
The "merging" or combination of dissonant elements forms the basis of a new, more extensive family classification, yielding the nine chord groups or "characteristic-types" below which are based solely on their dissonance content.
two elements 12, 16, 01, 26,
three elements 126, 012, 016, 026
all four elements 0126. (6)
Here "12" refers to the minor second and the major second, in whatever number of occurrences, as the only dissonant elements in a sonority, along with whatever consonances (which are excluded from the representation). "16" as a characteristic-type similarly refers to all sonorities whose only dissonances (with whatever consonances) are the minor second and the tritone.
Janeček is quick to point out the diminishing perception and effect of individual dissonances in the higher classes of chords (i.e. chords with more numerous members) to the extent that it is "practically useless to talk of the dissonant characteristic of complex multi-note chords." Conversely he notes certain singular "leaps in quality" or "clashes" (as opposed to "merges") in combining semitones and in combining tritones, thus substantially distinguishing 11 from 111, and 151 from the milder 121, 131, and 141. These harsher four-note combinations are recognized as equivalent in phenomenal significance to the dissonant elements themselves and are designated as the "semitone clash of semitone elements" and the "semitone clash of tritone elements."



Example 6a) the "increased" and "merged" semitone dissonances b) "increased" and "merged"
whole-tone dissonances c) "increased" and "merged" tritone dissonances

Example 7: The "Semitone Clash of Semitones" and the "Semitone Clash of Tritones"
Janeček's initial discussion of the combined or "merged" dissonances treats the whole tone as a secondary element to the more prevalent dissonant effects of the semitone, tritone and augmented triad. Judging by his four-note examples (Example 6), the whole-tone would almost appear to have the neutralizing or diffusing effect of a consonance. (7) The tritone in combination with other dissonances is heard to have a "softening" effect, "rounding off" any semitone dissonances and coloring the "grey blur of the chord governed by the whole-tone characteristic", and refining "the conspicuously penetrating augmented triad." (8) The augmented triad which obviously adds more tones than the other dissonant elements, is similarly heard to contribute "distinctively greater tension to the sound of a chord" which Janeček illustrates with the comparison of the 143(4) with the 314 and the (4)134 (i.e. dissonant characteristics 1 and 01) and the 332 with the 422 and 233 (i.e. dissonant characteristics 26 with the 026).
Discussion of the semitone and tritone "clashes" gives rise firstly to the
compound symbols 11 and 66, or a type of shorthand representation of the different
semitones or tritones which are, in both cases, joined by a semitone that is not directly
represented in the notational shorthand. (9)
The distinctive 11 and 66 clashes (orientation
schemes 11, 111 and 151) thus form the extremes among the merging dissonances with
the semitone in Example 6a, where the presentation is both systematic - as the diagrams
orient the "genuine increases" and the various "mergings" in a chromatically descending
bass-line against sustained upper-register components - as well as qualitative, in the
assessments of "very considerable worsening of the sound" toward the semitone or tritone
clashes, and "the sound becoming sweeter and more pliable" in the progressions away from
the semitone or tritone clashes. As the augmented triad is void of any genuine numerical
increase, and is limited in its generation of merging dissonances (to only the two structures:
13131 and the whole-tone scale, 22222), Janeček is able to restrict the scope of his
consideration of "higher order" dissonant elements to the semitone "clashes" of the
semitone and tritone. The Classification of "Harmonies" and "Characteristic-Maxima" In basing his classification of chord types on their dissonance content,
Janeček asserts the primacy of the dissonant "elements" in our perception of harmony. As
he later admits, however, while the presence or absence of dissonant elements may be
essential to the fundamental distinction of the wide variety of three-, four- and perhaps
certain five-tone "characteristic-types" (10) it is clearly diminished and compromised in more
complex sonorities. Janeček takes great care and deliberation to orient this aspect of his study in
relation to classical harmonic theory. The concept of a "harmony" in common practice
theory is taken as a precedent for his "characteristic-maxima", or the "heads" of his families
of dissonances and their respective "characteristic nuclei" or fundamental components. The
hierarchical distinction between "chords" and "harmonies" would appear to be one of style
as well as harmonic comprehensibility. As opposed to voice-leading or transient sonorities,
"harmonies" are seen as "independent", "intelligible" and "ranked higher than formations
of fewer pitches." The last of these refers to the "completeness," for example, of a C-major
triad, in comparison to the incompleteness of the major third C-E, or, similarly, the
incompleteness of a C-E-B sonority in relation to the completeness of the dominant
seventh CEGB. (11) Because of its lack of an essential dissonance however, the major triad
CEG could not be seen as an incomplete dominant seventh CEGB. Citing general
developments at the close of the Romantic period, Janeček further posits a process
whereby transient, or voice-leading chords could evolve into the independent harmonies
which came to populate the musical language of the twentieth century (see Example 8).
Example 8: Hypothetical Evolution of Dissonant Harmony from Voice-leading Sonority (H-
Harmonic Sonority, T - Transient Sonority) Janeček quickly realizes the limitations of applying traditional harmonic
classification strategies to the 350 chords (12) of modern harmony. Since the intuitive
distinction between harmonies and transient chords in modern harmony (which Janeček
does not elaborate) would still leave a vast inventory of chords, he must resort to factors
of "similarity" and "intelligibility". Here however he devises a different approach from
classical harmony since, while simpler chords can be heard as related to certain more
complex chords and not to others, the most complex chords (6 or more tones) do not have
the same intelligibility as the simpler ones. The representative "characteristic maxima" are
therefore to be taken from intermediate levels which are more complex than the
"incomplete" structures but more clearly intelligible than the "thickened" (13) structures. The
"characteristic nuclei", like the dissonant elements themselves (1, 2, 6 and 0) in the
classification of dissonance formations, are the "border formations" or irreducible two- or
three-note structures that maintain the essential qualities of the chord family. (14)
As will be
seen however, it is possible for there to be a number of different maxima for the same
nucleus and, in complex situations, there may be different nuclei for the same maximum. Here Janeček finally introduces a typographical distinction to differentiate the
characteristic-maxima from dissonance formations and orientation schemes. Thus "6" in
bold represents the maximum possible representation of the tritone dissonance
characteristic (which, as already seen in the unmerged increase of dissonances, is the
diminished seventh chord). The maximum 2 similarly is the quartal series of 5 tones
encompassing the maximum number of major seconds/minor sevenths (which is 3) without
involving any other dissonances. The sevenths themselves are then taken as the
characteristic nuclei for this chord family (see Example 9). (15) The next family is that of the characteristic-maximum 01 (orientation scheme
13131) which involves the maximum combination of the augmented triad (two occurrences)
and semitone (three occurrences) - its two nuclei, 134 and 314, containing only single
instances of these dissonances. The different semitone maxima 11, 12, and 13 are included
in the 01. As already seen, the augmented triad maximum (0) is already the augmented
triad which cannot be increased. The 026 maximum is the whole-tone scale which can be
reduced to six four-note (224) nuclei. The merging of the whole tone and tritone elements
has two maxima of different cardinalities, the five-note 261 (one tritone and three major
seconds) and the four-note 262 (two tritones and two major seconds), each reducible to 24
- 42 nuclei. The merged 16 and 016 share the same maximum 1331. As 016 it cannot
be decreased without losing a dissonance, so it is also a nucleus. The 141 and 133-331
subgroups are respectively 161, 162 and 163 with nuclei of 15 and 51. Two maxima obtain
for the 3-note nucleus 12: the six-note diatonic 22122 (four whole-tones and one semitone)
and the four-note 121 (two semitones and one whole tone). The "isolated maximum" 012
with orientation scheme 1214 (which cannot be decreased or increased) is closely related
to 122. With the characteristic-maxima 126 Janeček confronts a very complex and
inconsistent situation. Representing only the characteristic-maxima, of which five are six-note structures and the sixth the 7-note diatonic scale, and their 4-note nuclei, he notes that
the 7-note (diatonic) maximum does not contain all of the lower chords, and conversely, the
nuclei which are represented in the higher chords can only be found in some of the six-note
maxima. Janeček distributes the 7-note 0126s all as combinations of two triads plus one
note resulting in the dominant seventh-plus-major-triad shown in Example 9. 166 (the
tritone clash plus another resultant semitone) is discussed with 1266 and is not capable of
increase without adding the interval of the major second which gives rise to a 1266. As
Janeček notes, this maximum for both(166 and 1266) is familiar as the symmetrical
octatonic scale or combined diminished-seventh chords. Moving on to the semitone clashes, we find two 0112s and two 112s. 1126
however, offers a more complex family (with five maxima and four nuclei) of which Janeček
says the highest, 7-note and 8-note chords are too complex to be considered as
"harmonies." With the addition of the augmented triad to the configuration and the resultant
nine-note complex, Janeček begins to use "negative" representations i.e. "neg. (orientation
scheme) 22" for 11111122 or 01126. Combining clashes with the semitone yields 11266
which is closely related to (and now only negligibly distinct from) 1126 with a family of 6
maxima and the ultimate 011266 which is the 12-tone aggregate with 24 different 6-note
nuclei. In evaluating his classification families, Janeček immediately points out the
"loose" relationship of the subordinate chords to their corresponding maxima in comparison
with the relatively clear relation of complete and incomplete classical harmonies upon which
his classification is modeled. But he also admits connections between chords based more
on dispositions of essential sonority elements (i.e. the major triad), which can in turn relate
more complex sonorities which are unrelated by their dissonance and maxima schemes. In a putative counter example to his own system Janeček notes that the major and minor triads
themselves would be within the same boundaries in dissonance content (i.e. negative
dissonance content), as would all the maxima of type 126, despite their distinctive sounds. Example 9: Characteristic Maxima Chord Families (excerpts) Although this latter point is relatively undeveloped in the chapter, it is perhaps
the most challenging of all since it differentiates the roles of the dissonant interval content
and harmonic disposition in the distinction of complex chords. Retreating within his system,
however, Janeček goes on to formalize a notion of chord "boundaries" as an index of the
dissonances which are not shared between families. Between 16 and 6, the difference, for
example, would the "1" and the difference between 1 and 2 would be "12". Because of its
distinctive quality, a difference of "1" would be the most conspicuous. To this he adds the
"merging" effects of dissonances, so that a difference of 26 (because of the merging effect
of the tritone) would be less conspicuous than just 2, with similar relations for 1 and 16 and
0 and 06. Generally, Janeček concedes that such differences are further accentuated with
reduced numbers of tones and he concludes the chapter with another exhaustive table, of
all possible differences between the families, and, with the following example (Example 10)
listing boundary differences of dissonance involved in a chord-specific progression. Example 10: Example of "Boundary Differences" in Specific Progressions
Alternate Classifications: Triadic Combinations and Chord Disposition and Expression Because of what he terms "the rigid precision of the boundaries between
characteristic-types,
(where) sometimes it is difficult to see a definite boundary ....between
chords of different characteristic-types, and not to see it between chords of the same
characteristic-type" Janeček shifts radically from a classification based
entirely on dissonance
to one based entirely on consonance after Otakar Šin's chord types derived via combined triadic
functions. (16) Full combinations of two triads (for example, C-E-G/D-F#-A) are therefore like
characteristic-maxima in relation to the partial combinations where only the salient harmonic
pitches are present (for example, C-E-G/D-A). Janeček distinguishes further between "true"
combinations, where no common tones are involved in the combination (i.e. two major or two
minor triads separated by a major or minor second) and "partial" combinations where
common tones are involved between the triads. He forms four classes of combination: basic
uncombined triads, and true combinations of two, three and four basic triads. Since Janeček's first category ("uncombined triads") consists only of the
isolated major and minor triads and their three component intervals, it is only of systematic
interest. The second category involves twelve different combinations of major and minor
triads: six intervallicaly symmetrical (i.e. which combine the minor triad with its inversion,
the major triad, see Example 11) and six asymmetrical: +1+, -1-, +2+, -2-, +6+, -6- where
"+" and "-" refer respectively to the minor or major quality of the combined triads and the
integers in bold (1 to 6) to the difference in transposition (in semitones) between them. At
this point Janeček lists all the chords of the these families of which there are 95 (including
the different 12 six-note chords and the 2 "uncombined" major and minor triads) and
compares the families of the triadic combinations +2-, -2+, +3-, -4+ which are also
characteristic maxima. He notes the larger size of the triadic combination families and in
particular the chords of +2- which are not found in characteristic-maximum 12 and and those
of +3- which are not represented in 126. -4+ and 01 are found to have the closest
membership as they differ by the augmented triad (44) which cannot belong to the
dissonance family of 01 (since it has no semitone) but which represents -4+ since it
combines the major thirds and the intervals of difference of the two triads even though all
other chords in this triadic combination family contain a semitone.
`
Example 11: Representative Triadic Combinations and Dispositions Four- and five-note partial triadic combinations are treated as adjuncts to the
"true combination" harmonies for which Janeček develops a notational convention of single
and double arcs (for the number of common tones between the triads) above the interval of
transposition i.e. -4+ Such structures are then demonstrated to be subsets of the true
combinations by adding the particular two tones or one tone that will complete a "true
combination". The "true combination" of three and four triads becomes somewhat less
informative since the former generates twelve 9-note collections, none of which are
characteristic-maxima, and the latter generates the entire 12-tone collection. Nevertheless
the systematic subgrouping of the entire 12-tone aggregate into only two possible triadic
combinations -2-2+2+ and +2-4+2- is interesting and is listed with the 33 possible 11-, 10-,
9-, 8-, 7-, and 6-note family members which could be taken to belong to these two particular
triadic combinations (see Example 12).
Example 12: -2-2+2+ and +2-4+2- Subgrouping of the 12-Tone Aggregate Further discussion of the triadic combination schemes assesses the ambiguous
representation particularly of lower-order chords in two- and three-triad combination families.
Although it is generally unequivocal in its application, the obscurity of the scheme is
demonstrated by Janeček's own example. When the five-note GCF*AB (2221) and four-note
DC#EC* (112) are subgrouped into segments which contain no dissonant element (one tone
can be a subgroup) the result is two groups, FAC/GB for GCF*AB and three groups, D/C#E/C
or D/CE/C#, for DC#EC*. Thus the five-note GCF*AB is a two-triad combination and the four-note DC#EC* is a combination of three triads. Incomplete combinations are ambiguous in their
relationship to specific combination harmonies and since the very nature of triadic combination
is to assert two or more triadic roots for a sonority, incomplete sonorities in this classification
scheme reflect fluctuating identities between their different possible triadic roots, a situation
which can only be clarified in the harmonic disposition of particular sonorities, typically with the
more fundamental components placed lower in the registral distribution. Ultimately, Janeček asserts a complementarity between his characteristic-type
classification based on dissonance content and triadic-combination classification based on
consonance content. This complementarity however, is mediated by factors of chord
"disposition" and "expression" to which he devotes the entire fifth and sixth chapters of his
treatise. In a seemingly elementary digression, Janeček considers the voicing of a C-major
triad, reviewing traditional concepts of the "form" (i.e. "rotations" or which of the three tones
of the triad is in the bass), the "position" (i.e. which tone is in the soprano), and the inner
disposition of tones and pitch doublings. Stipulating that he is considering chords solely in
isolation (since many weak dispositions may be effective depending on how they are used
in specific progressions), Janeček arrives at traditional valuations such as "good",
"tight/wide/dispersed", "better", "bad doubling", "isolated 5th, 4th" with traditional caveats
against doubling thirds and advice for doubling fifths in 6/4 sonorities. In considering the disposition of consonant elements in dissonant chords
Janeček concludes that the location of consonances within these sonorities has virtually no
different effect than they would have in the consonant sonorities. Of the dissonant elements
1,2 and 6, it is only the semitone which, for Janeček, "reacts sensitively to disposition" and
he notes the essentially more favorable sound of the major seventh over the minor ninth,
and its "attenuation when spread over the maximum distance in any given sonority". Janeček finds however, that the disposition of the half-step in the context of
a major/minor third sonority (313 or a +0- triadic combination) sounds notably more
dissonant as a semitone or a minor ninth in comparison with its sound as a major seventh.
He further makes the very interesting observation that in any dispositions of a 213 sonority
the semitone sounds equally good and that in more complex sonorities (of 5 or more notes)
"containing the chord 313, the difference in sound between various dispositions of the
interval 1 will be substantial, while in the chords containing 213, it will be negligible." In
others instances the difference between placements of the semitone (or major seventh or
minor ninth) is designated as "average" and less pronounced than in the contexts involving
either a major/minor triad (313) or the incomplete dominant seventh/minor ninth sonority
(213). "Cluster" chords, containing interval 2 as major seconds, are regarded as predictably
"bad" dispositions which can be "improved" by re-disposing the pitches of the chord as in
Example 13. Example 13: Varying Dispositions of 313 and 213 Groups Returning to his classification of triadic combinations, Janeček affirms the
importance of the lower triadic component whether the triadic components are separate or
mixed (17) (i.e. "combination" or "non-combination", see Example 14) as a (harmonic)
"determinant" or basic sonority for the entire chord. If this "determinant" contains a minor
triad belonging to a 313 subgroup, the disposition will be "very bad"; if not, it will be any of Janeček's shades of "better" depending on the disposition of other 313 groups or the
presence of as 213 group. Based essentially on his 313/213 principle of dissonance
disposition and a number of intuitive considerations, Janeček goes on to schematize the
dispositions of both "true" and partial triadic two-triad combination classes (combinations of
two triads i.e. +3- etc.) into "good" and "bad" dispositions depending on which harmony is
lower (i.e. the determinant) with various comparative comments such as "disposition 2nd/1st
is not entirely bad". One can only be impressed by Janeček tenacity in proceeding to three-triad combinations and even four-triad (12-tone) combinations providing discussions which
undoubtedly have been an inspiration to many young composers, but which lack more
refined considerations of harmonic progression, dynamics and scoring to be relevant to
practical compositional circumstances. Example 14: "Combination" and "Non-Combination" Sonorities with Sample Commentary from Janeček's "Combination Dispositions of Harmonies II " Indications of "1st 2nd" etc. refer to the relative registral positions of the triads, i.e. the first triad is in the bass or lowest register and the second in an upper register. In turning to the "expression of chords" Janeček begins a larger discussion of
harmonic progression with considerations of the linear connectedness of individual tones.
He distinguishes between "real tones" which are the sounding tones as we hear them, and
"imaginary tones" which are real tones after they have sounded and remain in our immediate
memory before being connected to the real tones of subsequent chords. In due course
"imaginary pitches" will either become linearly connected to a subsequent tone (for which
Janeček applies the term "cancelled") or they will "die out". Janeček's three conditions of
connectedness and (or "cancellation") of imaginary tones are the "appearance of a real pitch
a semitone higher or lower" than the imaginary pitch or "the appearance of a real pitch a
whole tone lower" than the imaginary pitch. "Cancellation" via a real pitch a whole tone
higher is admitted only if the imaginary tone is structurally weaker than the canceling tone
i.e. if it is unemphasized, less metrically prominent, or itself preceded by lower neighbor tones. A "counter-canceling" pitch is a pitch which prevents an imaginary tone from
being cancelled by a real pitch a whole tone above or below. This pitch must be a semitone
distant from the imaginary tone but need not be in the same octave. The "counter-canceling"
pitch thus interferes with the normal continuity which would otherwise arise from the whole-tone connection. The effect of this denied connection, however, which leaves the imaginary
pitch, "in the air", as it were, is to accelerate its dying out which Janeček indicates by lines
of decreasing thickness (see Example 15) with a descending hook at the end. It is
interesting to read Janeček's assessment of the stylistic difference between classical and
modern composition in terms of these phenomena: For classical composers, the progressions ... are unacceptable; they are "impurities". ...In
contrast, modern composers at times even seek out such two-voice and single-voice
progressions ... In the final analysis, both attitudes spring from the same cause: acute harmonic
entanglement. While classical composers avoided this as stylistically impossible, modernists
seek it out as something "unheard," as something that has not yet been used to its full potential. (18)














Example 15: a)
Graphic Representation of Canceling and Dying-Out of Imaginary Pitches, and b) Counter-Cancelling Pitch
Concerning the slow, normal and accelerated dying away of an imaginary tone, Janeček surmises that this depends on the harmonic context established by the preceding pitches. Preceding tritones or consonant intervals afford a more lengthy dying out of the imaginary tone. The major ninth, minor seventh below or major seventh/minor ninths above allow imaginary tones to die out at the normal rate. The rate of dying out is accelerated however, when the imaginary tone is preceded by a major seventh or minor ninth above. The general principle governing cancellation is that lower pitches facilitate the dying out of imaginary harmonic tones more so than higher pitches. Subsequent pitches similarly affect the dying out of an imaginary harmonic pitch in the same way as preceding pitches. Superimposed tritones and consonances will enhance (prolong) the harmonic "decay" of an imaginary tone more than major ninths/minor sevenths, and descending minor sevenths/major ninths will in turn allow longer "decays" of imaginary tones than those dampened by descending major sevenths/minor ninths.
As can be assumed from his choice of terminology, Janeček's interest in "imaginary tones" lies not so much in the realm of tonal syntax but in the phenomenon of the individual sonority and its apparent perseverance in the ear until it is succeeded partially or completely by the next sonority. In addition to studying the harmonic state of chords as determined by "real" or "imaginary" pitches, Janeček cites the even richer possibility of characterizing the chords generated at the interphase of real and imaginary chords i.e. the lingering pitches with those that are newly arriving to the ear. He gives various examples (see Example 16) in which he employs a combination of the notated harmonic progressions with a superimposed typescript of the imaginary tones and the linear graphic representing their projected decay.

Example 16: Progressions Involving the Interaction of Real and Imaginary Pitches
Situations involving chords larger numbers of pitches pose less substantial impressions as imaginary pitches in Janeček theory since they will inevitably be "cancelled" in the dampening complexity of the ensuing chord. Similarly the interference of imaginary tones is much greater in the succession of consonant sonorities than in the succession of dissonant sonorities and hence the need for classical voice leadings to nearest adjacent pitches which will eliminate the accumulation of imaginary pitches. Janeček explores other implications of cancelled and uncancelled pitches in the silence following staccato chords or quick arpeggiating figures and the "dampening" affect of close-proximity dissonances as opposed to consonances or in widely spaced dissonances.
The situation of the "composite expression of chords in a single voice" (Janeček's expression for compound melody) provides a further dimension of Janeček's theory of the "imaginary" tone in the implied harmonic structure of a single-line melody (see Example 17).

Example 17: Harmonic Profile of Single-Voice Melody
In parsing more complex situations Janeček adheres to more or less intuitive preferences: for two (or more) simple chords as opposed to single, more complex sonorities, also for simpler metric parsings over more complex ones, and for harmonic segmentations that complement rhythmic motivic structurings. He acknowledges the ambiguity of many modern melodic situations where clear segmentations, even of just the real pitches, are not possible.
Janeček's discussion become particularly refined in the consideration of non-harmonic tones versus "counter-canceled" tones (which involve a dissonant harmonic structure) and "imaginary harmonic" versus "imaginary tonal" (essentially the common-practice non-harmonic tones) pitches. The latter are more transient, more linearly connected, less disruptive of the harmonic context (i.e. invariably "cancelled") and hence insignificant intrusions on dissonant formations. Among the more prominent effects of non-harmonic tones, he notes the very "penetrating" and de-tonicizing effect of passing (non-harmonic) tritones formed with whatever degree of the consonant triadic structure, and also the less structurally threatening effect of dissonances forming a whole-tone or a semitone (but not also a tritone) with whatever member of the triad. Janeček attributes this to the innate attraction of the tritone, as if the ear wants to keep it as part of the harmonic sonority. Only the major/minor third semitone alternation is judged to have comparable distracting qualities to the passing tritone. Generally, because of their inherent connectedness Janeček ascribes a greater "durability" in the overall tonal/harmonic percept to "tonal imaginary" pitches (passing tones etc.) as compared to "harmonic imaginary" pitches since they function at a lower, more sustainable level of our harmonic awareness.
The "incompleteness" of harmonic sonorities is also an aspect of their particular "expression" and one interesting consequence Janeček's concepts of "tonal" and "harmonic imaginary" tones is his conjecture that incomplete sonorities are more "inclined to take in spontaneously further components by which they can be enriched." Dissonant formations with few tones will conversely tend to take in pitches which will not complicate their dissonance characteristic and more consonant incomplete chords will strive toward completion via their transient tonal and imaginary pitches.
Speculations on Harmonic Motion, Function and Progression
Janeček's initial distinctions among possibilities of harmonic motion are those of "partial harmonic motions", between chords of similar pitch (but not dissonance) content and "fundamental harmonic motions" between two clearly independent harmonies. "Higher-ranked" harmonic motions are designated as the more pronounced motions between the end of one chord succession and the beginning of the next. "Links" are common pitches between adjacent chords, and can be single, double or multiple and even "complete" in the case of identical repeated chords in which there is no harmonic motion. A "direct link" is a direct pitch repetition or, interestingly, an octave transposition which does not "cross over" or take part in a major or minor second voice-leading (19) anywhere in the harmonic motion. An "indirect" or interrupted" link conversely involves an octave transfer which does not cross over a major or minor second voice-leading. Generally, direct links form stronger bonds between chords than indirect links and the fewer the pitches in the chord, the more effective the link (see Example 18).

Example 18: Examples of Direct and Indirect Links
Essentially what Janeček judges in his category of harmonic motion are effects of succession and continuity between tones related in purely harmonic terms. Partial harmonic motion lies between melodic motion (i.e. the absence of harmonic motion) on the one hand and fundamental harmonic motion on the other. Whereas melodic motion is seen to unfold harmonic structures via uncancelled imaginary tones, partial harmonic motion will result from the cancellation of some imaginary pitches in a first harmony via real pitches of a second. Fundamental harmonic motion, however, will result only from the simultaneous cancellation of all imaginary tones between successive chords.
Relative judgments as to the effectiveness of the link, and hence whether a progression is "fundamental" or "partial", depend on the number of tones involved in the link (a single tone for two voices, a double link for three or four voices, a triple link for five voices etc.) and the harmonic/registral strength of the link, i.e. whether it is in the bass, etc. What is judged to be an insufficient link between two harmonies gives rise to a fundamental harmonic motion or the succession of independent harmonies as opposed to merely successive states of the same harmony, or in Janeček terms, "interdependent chordal cross-sections". Janeček gives multiple examples of partial and fundamental harmonic progressions in which tones between chords involved in voice-leadings of 1 or 2 semitones present a "pronounced" form of harmonic motion. Uncancelled imaginary tones of course, complicate the situation but generally Janeček asserts that the "simpler intervals" formed between imaginary tones of the first chord and the real tones of the next will make the more effective harmonic function. Imaginary pitches (which, as such, form "imaginary" links between harmonies) will not effect the status of a progression as "partial" or "fundamental" except with wide ascending leaps in all voices (and hence multiple uncancelled imaginary tones) which would tend to link the chords as a single registrally unfolding harmony.
Interesting postulations emerge in Janeček's discussion of voice-exchanges or indirect links via register transfer of tones between chords. While the impression of a more fundamental progression involving these effects is difficult with three-note chords (see example 19a), he notes that it is possible with four- and five-note chords. Among indirect links the case of the common tone becoming part of a melodic interval 1 or 2 (as opposed to crossing it) is a more significant link. This case is weakened if it is part of a voice-exchange, i.e. the melodic movement of 1 or 2 semitones is reversed in another voice. Fundamental harmonic motion is said not to be possible between two different positions of the same transposition of consonant triads or dissonant three- or four-note chords that do not contain the interval 1 or 2 (i.e. 44, 33 or 333). But a fundamental harmonic progression is said to be possible between different chord types or different transpositions of the same chord type, and also with different registral dispositions of the same transposition of higher-class (4-, 5- or 6-note) chords containing the interval 1 or 2 (Example 19b and c). Especially interesting in the latter case are the voice-exchange progressions of two-triad combinations. Re-voicings of +2+ combinations (major triads separated by a major second) are not seen to produce fundamental harmonic motions to the same extent as, for example, the more complex +6+ re-voicings.

Example 19: "Fundamental" Progressions Involving Registral Exchange of Pitches
In an essentially normative discussion, Janeček acknowledges the relation between rhythm, meter and fundamental harmonic progression and the role of effective modulatory chords in "higher-ranked" harmonic motion. Cadential progressions then become a standard for judging other progressions in terms of three factors: the "pure" tonic, the leading tone and the functional principle. The "pure" tonic as an ultimate sonority is free from imaginary pitches, or pitches that have not been connected to the tonic by half step or descending whole step. Janeček however, adds a further condition that the "pure tonic" be free from imaginary tonal pitches (i.e. unresolved non-chord tones) which form a tritone, the most "welcome" dissonance, with any of the real pitches of the chord. In other words, in C major, the chromatic tones of C#, F#, and B. Janeček does not discount the possibility of final cadences which are less tonally closed or which even end on dissonant sonorities, but rather asserts the pure tonic as a universal ideal operating on a higher level than stylistic convention.
Concerning the pre-cadential chord Janeček notes that of the nine notes of the negative of the major triad, three form tritones with the different degrees of the tonic triad (B, F# and C#, for a CEG tonic) of which one cannot be cancelled (B) in motion to the tonic triad. The other two, (F# and C#) can be resolved via semitone motion (and hence cancelled) into the tonic, but the F# is a less appropriate pre-tonic element since it forms a tritone with the tonic pitch itself. In the minor key, A natural is eliminated as a pre-tonic element since it would form a tritone with the minor third (E). Janeček asserts that there must be one semitone cancellation in cadential harmonic motion, with obvious preference for the one to the tonic pitch itself. A descending half-step motion (D - C), however, would evoke the tritone with the fifth (G) of the tonic sonority and a second leading-tone, to the fifth (F#) would similarly conflict with the tonic itself, as already noted.
Janeček's theoretical discussion of the functional principles of harmonic tonality echoes the symmetrical balancing of "pre-tonic" degrees above and below the tonic as seen in the dominant and subdominant of the theories of Riemann and Otakar Šín. Thus Janeček maintains that only the purely consonant and hierarchical (root/third/fifth) harmonic structures of triads are capable of defining a functional tonal space (20) and that the only admissible pre-tonic triads should have equal but opposite functions and mutually exclusive pitch content among themselves. They should also fulfill a fundamental harmonic progression with no more than a single tone in common with the pure tonic. Thus, the voice-leading principle of the pure tonic, i.e. the resolution of all imaginary and melodic tones, will admit only the dominant and major and minor subdominants as pre-tonic sonorities (for major or minor), and so idealizing the "classical functional system of three members" which comprises the nine pitches (including E of the tonic minor, and the A of the minor subdominant) of the combined major and minor scales.
To accommodate the harmonic and tonal resources of new music, however, the classical three-member system is expanded to five members including the flattened supertonic (Phrygian) and major leading-tone sonorities (Lydian) which maximize the semitone voice-leading to the tonic. The new degrees are designated respectively as P (D-F- A in C major) and L (B-D#-F# in C major) for their contribution of the Phrygian second and Lydian fourth. The flaw, as Janeček sees it, in the new pre-tonic harmonies is in their tritone relationships with the tonic itself (the Lydian fourth to the tonic and the Phrygian second to the fifth). As a solution to the problem of integrating these harmonies into the syntax of the "pure tonic" Janeček proposes the progressions PLT (Phrygian to Lydian to Tonic) or LPT with the minor Lydian which eliminate unresolved imaginary tones through the voice-leading successions of semitones. Similarly, the new pre-tonic harmonies (P, L) are strengthened when they are joined to the classic pre-tonics S, D (Subdominant and Dominant), i.e. PST, PDT, LST, LDT, canceling the tritone imaginary pitch arising from P or L with the tonic itself.
The final portion of Janeček consideration of pre-tonic function concerns the ambiguity of dissonant two-, three-, four- and five-function combination chords (composed by combinations of the five major and minor T, D, S, P and L functions). From the multitude of all possible combinations, some (i.e. -+D/-T, -D/+T etc.) are eliminated because they "encumber" the progression of the pure tonic with too many imaginary tones. Others, such as -P/+T, are redundant as they result simply in a missing note from more complete combinations such as +P/+L. Further redundancies are eliminated between combinations of two functions (-L/T, for example) which produce an incidental third function (+D) thus significantly reducing the number of larger member combinations. Of the 74 admissible and non-redundant major and minor combinations, only 19 are seen to be unambiguous, i.e. referable to a single tonic and are listed with their orientation schemes. A subsequent list is then presented all of the ambiguous combinations with their orientation schemes and pitch examples with the keys to which each sonority can be referred as a combination of harmonic functions (see Example 20).
Example 20: Excerpt from Janecek's List "Ambiguous Dissonant Functional Combinations"
As is often the case in this work, the attention given to the generation of the
analytical typologies is far in excess of any discussion of their analytical significance.
However, based on their typical frequency of occurrence and distribution, some integrative
considerations of proximity and family relationship between the 5 functions are offered as
in Example 21. The dots indicate closeness of relation as might be seen in Schoenbergian
structural functions and tonal regions. Janeček notes additionally that factors of concrete
disposition and completeness are essential determinants of functional intelligibility and
proximity of these abstract schemata:

Example 21: Representation of Family Relation of Tonal Functions
Janeček further develops the notion of inter-function (IN) or chromatic triads which are viewed as combinations of both tonic and pre-tonic functions for which he suggests particular symbols to indicate which pitches are borrowed from which functions. He then proceeds to break down the inter-functions of all major and minor triads in relation to C major: thus in C major, the A major triad, or IN3, would be an inter-function of subdominant and minor Phrygian functions. (21) The tonic can have direct or indirect relations to inter-functions, depending if they proceed to other chords before reaching the tonic. Ultimately, in Janeček's view, sonorities can be derived as combinations of elements from tonic and pre-tonic chords. With the inclusion of the minor dominant and Šin's P and L functions, all 12 tones would be available for this, and so any dissonant formation could be related to a tonic S a theoretical possibility, as Janeček admits at best. Nevertheless, another categorization of dissonant formations is proposed based upon four possibilities: superimposed complete functions (the dominant upon the Phyrgian, for example), triads supplemented with single pitches from another function (dominant plus the basic pitch of the subdominant), functional degrees merged with inter-functional triads (i.e. the dominant plus the major mediant, or +IN4) and finally a group like the inter-functions which combines single or double elements from various functions. While superimposed complete functions are clear in their implication, the actual functions of the more fragmented and mixed combinations can only be determined from the musical context (see Example 22).

Example 22: Examples of Fragmented Functional Combinations (excerpt)
In his preliminary notions of harmonic progression, Janeček creates several categories and differentiations which can be schematized as follows:
Motion: quality of harmonic motion: primary and auxiliary functions / tonal direction levels of motion: lower, higher and intermediate
Function: "resolution": "lower" or "higher" levels "connection": "simple" or "compound" and "lower or "higher" level "transfer"
The "quality" of harmonic motion relates previously established primary versus auxiliary functions (Tonic, Dominant, Subdominant versus Phrygian and Lydian) to the notion of direction to or from the tonic, dominant or subdominant. (22) "Higher" levels of motion are attributed to movements between primary and auxiliary functions (Pr - Aux or Aux-Pr) and lower levels to movements within primary and auxiliary functions. Intermediate functions are conceived for progressions between combinations of primary and auxiliary functions. "Resolution" refers to harmonic motion directed to the tonic, which can be "simple" (as in triadic motions) or "compound" for variations or derivations of this motion, with the possibility of harmonically imperfect resolutions to the tonic (added sixth sonorities, for example). "Lower level" resolutions involve motions of primary or compound functions to the tonic with "higher level" resolutions involving the auxiliary functions moving to the tonic. "Higher level" resolutions are thus said to be weaker than those involving S, or D, or elements of S or D.
"Connection" is the opposite of resolution; it refers to a motion to a function other than the tonic. It is "simple" if it involves only single functions and "compound" if it involves combined functions. "Lower level" connections, again, involve movement within primary or within auxiliary functions and "higher level" connections involve movement between primary and auxiliary functions. A "transfer" is a special case of harmonic motion where a composite sonority is reduced to one of its component parts, typically involving uncancelled imaginary tones. Janeček summarizes these relationships in terms of the functional degrees in the following diagram (Example 23):

Example 23: Janeček's Summary of Resolution, Connection and Transfer Relationships
Concerning harmonic syntax Janeček offers essentially common-practice intuitions by which the simplest and most intuitive analysis is the most desirable, and by which the awareness of the tonic is established both by its physical prevalence and its inherent "gravitational" relationship to the functional progressions. Having said this, however, he presents a number of passages of theoretical interest as "successions of complex chords with rich sounds and considerable kinetic tension". The examples which Janeček gives are worth representing in part here since they further illustrate the stylistic milieu which seems to have given rise to his concepts of progression and function. (23) In one example (see Example 25 below), he substitutes different resolutions for the penultimate sonority as well as different openings, demonstrating the flexibility of his materials and providing interesting cases where the tonal context prompts different readings from what might be imagined for the chords in isolation.

Example 24:
Janeček's Progressions Involving Complex Functional Relationships (excerpts) Janeček's treatment of functional bitonality and polytonality is perfunctory and essentially normative as he ascribes only rare occurrences to the phenomena (i.e. two or more keys simultaneously). He subsequently acknowledges the possibility of resolution to non-pure and even complex and dissonant tonics with the caveat that the process of functional gravitation be necessarily clearer than might be sufficient for consonant tonics. On the issue of altered functions, Janeček notes that -D (in the major) and +S (in the minor) have clear identities but, avoid the pure tonic leading-tone and furthermore create tritone associations in their progression to the tonic sonority. Minor dominants for Janeček, however, are not unwelcome as applied dominants since they do not introduce chromatic tones which are foreign to the key (24) as in the descending cycle of fifths T (d) (d) (d) D T. The rising cycle of fifths (FM, CM, GM, dm, AM), is conceived as a series of applied subdominants, and would be represented S (S) (s) -S +T. (25) The difference between the minor applied dominant (d), and the inter-function -IN2 (the minor second degree inter-function of the major key) is the directionally neutral quality of the inter-function.

Example 25: "Modulation from D major to B minor Without Real Asserted Pure Tonics"
In a very interesting commentary, Janeček contemplates the effectiveness of modulation in terms of the variety of ways in which the tonic can be harmonically weakened and then disrupted, thus imparting not only a degree of uncertainty in the tonal orientation but also a certain "novelty" and "freshness" in the prevailing harmonic syntax. The typical weakening agents of the applied functions, the auxiliary functions P and L, the inter-functions (in isolation or combination) and bi-tonal or polytonal chords are integral to the essential "renewal" and maintenance of harmonic interest which Janeček describes in these transitional passages. This, he claims, gave rise to all of the increasingly ambiguous situations, systems and modulatory practices of the late Romantics such as the cadential use of the half-diminished sonority in the close of Debussy's Afternoon of a Faun and the use of the church modes in Vítslav Novák's "Prelecel sokol" from his Slovenske spevy. In Janeček's view the extreme case of the avoidance of the tonic obtains in "non-functional (atonal) music" (26) where either the gravitational attractions of the tonic or the distinctiveness of the tonic itself are destroyed. It is perhaps no surprise, however, that Janeček insists that "reliable functional relations can be found in music intentionally created as atonal." He asserts, for example, a "masked" B minor in Example 26a and a C major with an elided final E-minor tonic in Example 26b, an upper G minor strata in Example 26c, and layered function in B major in Example 26d. Janeček's closing comments on the issue of atonality suggest parallelism, full chromaticism, non-combination (i.e. quasi-bitonal) chordal dispositions and limited diatonic progressions as means of supporting "non-functional comprehension".
In a particularly revealing discussion, Janeček seems to touch on his essential
view of musical language. His notion of "styling (27)" in modern harmony refers to the
conscious compositional choice of harmonic materials within classical harmonic idioms such
as parallel motions, pedals, doublings, contrary chorale-style motions, imitative contrapuntal
techniques, etc. Thus Janeček, as much as any other pre-war European composer,
adheres to the pouring of the new harmonies into the neo-classical molds, and to the
exploration of personally conceived recipes and definitions of materials, forms and harmonic
syntax.
Example 26: Examples of Functional Relations in Atonal Contexts
In his chapter on "problems and applications" Janeček sketches a philosophical, and almost pan-historical perspective in which "modern harmonies" (the chord types themselves) created a radical divide between contemporary musical languages and those of the baroque, classical and romantic eras. Yet at the same time he sees that they are guided by the same principles of harmonic succession that evolved in the earlier styles. In essence, however, "modern harmony" is also a repository which also includes the chord structures from the past eras. Thus Janeček sees the necessity of distinction between universal laws, as best they can be expressed and which apply under all circumstances, and the evolving stylistic tendencies of certain eras and certain composers.
He takes the very engaging stance concerning the pre-eminence of the creative act that "the law of an artistic work is sufficiently autonomous that a discrepancy with established law in the realm of art is of no consequence to it; neither is a discrepancy with any natural law of any importance..." Janeček cites the historical discovery of perspective in visual arts as an obvious natural principle which invalidated neither any previous artworks nor subsequent works which were eventually independent of its principles. In the musical domain, he cites the Landini cadence in its indirect motion to the octave (scale degrees 7-6-8) which can be seen as an altered precursor to the more direct voice-leading of the DT "pure tonic" (leading-tone to tonic) formula, is also seen to persist in its own right as a distinctive cadential idiom in subsequent eras. Following this view, Janeček concludes that the chromatic and diatonic systems are natural systems, whereas whole-tone and quarter-tone systems are artificial or only partially natural etc.
Janeček expounds at length on the necessary integration of experience with theory citing treatises of Skuherský (28) and Hába as examples of work dominated by the experiential without the organizing strength of conceptual insight. Primary experiences in Janeček's view must be transformed within reason into principles, and two or more principles, even apparently disparate principles, can be subsumed under a common denominator. The defining qualities of Janeček's "pure tonic", for example, are related to the particularly attractive and stimulating quality of the tritone in isolated chords which is avoided in a closing sonority. Thus phenomena which appear unrelated (i.e. the sensual quality of the tritone and the tonal stability of the perfect cadence) will eventually become fully or partially assimilated into more inclusive principles. Throughout the course of the treatise, Janeček inadvertently provides many such illustrations of this: his orientation versus harmonic scheme, the characteristic-maxima versus triadic combination families, etc.
Janeček provides a rigorous assessment of the dual nature of harmony as eminently static in quality and kinetic in effect, thus making it impossible to consider motion (functional progression, imaginary tones etc.) independently from the uniquely affective dissonant/consonant qualities of the chords involved: "their tension versus their functionality (i.e. their possibility instead of their necessity). Phenomena such as imaginary tones are at the inter-phase of tension in the succession of sonorities since they represent lingering, unresolved voice-leading tensions." Janeček even seems to raise elementary formulations of a "kinetic" concept of harmonic progression in the succession of dissonances:
This does not say that in actual cases conditions are not more favorable for one particular goal or direction (of a progression) than for other goals and directions. These favorable conditions depend on the measure of motion necessary to reach the goal.
Thus Janeček sees that in their ambiguity of dissonance and function, modern harmonies are particularly sensitive to the most subtle effects nuance and disposition. The extreme (and for Janeček, rare) case of non-functional harmony assumes that "internal and external tension, dissonance and the non-tonic quality are one and the same" and would give rise to a situation in which 'the most favorable' kinetic possibilities have disappeared and all possibilities are 'equally good'"
In his chapter on "Compositional Practice" for which he provides extensive examples, Janeček explores more deeply his compositional and pedagogical concept of "styling". His main concern here is for composers, and in general that "if they want to defy some traditional law, for example, they do so in a way that will not appear as lack of skill". His essential starting point is "harmonic phenomena that can be judged statically without considering their relation to their surroundings" to which he gradually adds "phenomena that are explainable kinetically."
Beginning with the creation of "modern melody" Janeček like many other compositional theorists, advocates recipes for avoiding the clichés of diatonic or chromatic melodies, i.e. resolution of leading tones, specific rhythmic figures, the typical connections between identifiable harmonic functions, etc. (see Example 27a). Then, broaching the harmonic context, melodies are written with counterpoints or accompaniments restricted to major or minor diatonic triads (Example 27b) or a specific interval (the perfect fifth, Example 27c) and with varying degrees of chromatic accompaniment, contrapuntal complexity and dissonance and focused on particular intervals or harmonic structures (with particular attention, as in Janeček's Chapter 5, to the disposition of all 1 intervals or 01combinations). Initial exercises explore simpler combinations followed by denser combinations (16, 016, then 126 etc.) and an "exercise on a given harmonic basis" makes a two-voice adaptation from the chorale passage of Stravinsky's Three Compositions for String Quartet (Example 27d). This is followed by the inverse exercise of deriving a 5- or 6-voice harmonic background from the opening measures of the third movement of the Suite for piano of Pavel Bokovec and then a recomposed imitation of the original from the harmonic sketch. An extensive exercise ensues in setting a short seven-note melodic fragment involving different harmonic skeletons (chordal regions, in legato sustained sonorities and in stacatto arpeggiations), different mid-register counterpoints, chord-stream accompaniments and descants - all hosting a variety of harmonic challenges and points of dissonance treatment but with the general goal of ensuring "that the sonic effect of individual chords was good and that there was an overall natural flow"
In his texture exercises Janeček provides two- and three-voice accompaniments for a simple flowing eighth-note phrase, with different harmonizations for each which nevertheless retain certain common harmonies. Accompaniments proceeding in wider leaps were seen to leave more residues of imaginary pitches than others and hence were deemed to be harmonically richer. The complex issue of the resolution of dissonant sonorities is approached with registrally distinct triadic components (i.e. "non-combination" dispositions) and then through dispositions in which triadic components are intermingled (i.e. "combination" dispositions) with the aim of finding different solutions and classifying the results in terms of the harmonic function of the chord to be resolved.

Example 27: Examples of Compositional Exercises
In the resolution of combination dispositions we see various principles at work
including the unfolded 11 group in Example 28a which obviates the normal voice-leading
resolution (ascending major second resolution for the D natural). Other aspects of
resolution involve inter-function sonorities which in principle are obliged neither to obey
pure-tonic voice-leading nor to be balanced by primary functions (Example 28b).


Example 28a: Unfolding of a 11 Example 28b: Example of Inter-Function
Voice-leading Resolution
Voice-leading Resolution The pursuit, on the other hand, of a pre-tonic chord for resolution must ideally
balance components of D or L with S or P. Disposition become paramount in Janeček's
sampling of instances (see Example 29) in which the single leading tone counterbalances
the entire S, as well as a complex 6-note chord in the third case and a particularly harsh
sonority in the third and fourth examples.

Example 29: Various Pre-tonic to Tonic Resolutions
Resolution is strengthened by altered or closely related repetitions of pre-tonic chords
successions (Example 30a) and by strings of pre-tonic chords, each suitable to resolution
on the ultimate tonic, which may be strung together with only the final chord providing the
actual resolution (see Example 30a and b).



Example 30: a) altered versions of the same pre-tonic chord b) succession of pre-tonic chords to the ultimate tonic c) possible resolutions to final tonic of the pre-tonic chords in b)
The actual progression from the pre-tonic sonority to the final tonic may be "strong" with
pronounced linear or harmonic motions in the bass (i.e. clearer DT functions without
"uncancelled " "imaginary" tritones in the voice leading) or "loose" or less clearly defined
(Example 31).

Example 31: Example of "Strong" (a) and "Loose" (b) Relations to the Tonic
Chords with clear tonic resolutions will dominate a passage at the peril of becoming too obvious and hence the value of controlling the more obscure functional relationships. Janeček attributes a particular "centrifugal" value to chords that can be favorably resolved into "other" tonics and as such stand close to the category of "chords that defy the tonic completely." The discussion grows particularly inventive in its consideration of "functional variations in a chord progression" where Janeček provides a very rich and varied series of cadences or pre-tonic sonorities and resolutions (Example 32).
Example 32: Variations on Dominant-Tonic Formula
Despite the sensitivity of their voice-leading and functional balance in their resolutions, it is curious that few of these resolutions are acceptable to the ear because of the simplicity of the pure tonic triad in contrast to the remarkable richness of the pre-tonic sonorities. Janeček's subsequent variations applied to harmonic phrases, however, involve initially complex tonics, followed by complex subdominants, dominants etc., but once more, resolve to inappropriately simple, and perhaps only theoretical tonics. A final set of variations adds chromatic bass lines to the functional formulas defined in the upper voices.
In turning to "free composition" Janeček offers an interesting example from his own composition Variations op.25 in which clearly combined functions as well as a pure tonic enclose a 10-measure arch of the melody with certain resolving complications. Subsequent, more refined examples come from his Sonata for piano op. 25, but with surprisingly little commentary apart from remarks on foiled harmonic expectations, "open-ended phrases" and bitonal interventions of a remote tonality (F minor) against the tonic (D major) in one of the more transparent and lyrical passages. It would appear that other passages are left for the reader to make his own observations concerning technique and harmonic function.
In an example which must be close to his own harmonic thinking Janeček demonstrates the accessibility of atonal chorale styles to the tabulation of orientation scheme and dissonance characteristics (Example 33).

Example 33: Application of Orientation Scheme and Dissonance Characteristic Analysis to a Chorale-Style Excerpt
Janeček is particularly intrigued by the effect of the second chord in the second measure which contains an unfavorable disposition of the F-F#. His explanations are insightful yet surprisingly non-harmonic as he points to the uncancelled A natural which would enrich the F-F#-E=-B sonority and the fact that the 421 is much richer in its 126 dissonance than any of its surrounding chords. A two-voice passage in the same style (Example 34) demonstrates a conscious preference for dissonance characteristic 1 which, despite the minimal instances of imaginary tones provides a number of challenges for his "chordal cross section" and the discussion of "chords of composite presentation."

Example 34: Application of Orientation Scheme and Dissonance Characteristic Analysis to Two-Voice Excerpt
Two of the analytical goals which Janeček sets for his theory are the elementary discernment of whether particular chord-, or characteristic-types, or dispositions appear exclusively or pervasively in a particular passage and whether the expression of the essential chords has any metric ambiguities. This is accomplished in obvious ways in the preceding chord- and dissonance-characteristic profiles beneath the harmonies but also in the study of transient or non-harmonic chords among the analyses which are listed with commentary in Appendix B. Janeček's closing overview of the issue of the "tonally functional plan of a composition" asserts an essentially normative distributional view of modulation, affirming the tonic at the beginning and end of a composition as an essential framework within which secondary keys can be expressed in various degrees of clarity or complexity and functional (primary or auxiliary) representation. He then hypothesizes cases in which remote modulations could involve keys expressed in essentially primary functions in contrast to very close modulations involving keys expressed by very complex and auxiliary functions.
Commentary
Although it has been possible to do little more than skim the surface of Janecek's work, it is hoped that the preceding overview of the Foundations of Modern Harmony will prove of some introductory value in our expanding historical and technical understanding of twentieth-century theory and composition. Its significance is obviously unquestionable in the development of Central European compositional esthetics and while the details of Janeček's theories may be unique and personal, they clearly complement the fluid and intuitive harmonic languages not only of Martin, Isa Krejčí, Vítêslav Novák, and Janeček himself but also the comparable languages of Roussel, Hindemith and Honneger, to say nothing of the subsequent generations who has been influenced by Janeček's own teachings.
Other aspects of the treatise's unique cultural "location" referred to at the onset of this study can be seen in its legacy of functional tonal analysis in the line of Riemann via Šin, its (albeit disavowed) adaptation and development of Leoš Janácek's concept of the "imaginary tone", and the apparently original inception of a harmonic prime form (the "orientation scheme") long in advance of the analogous and eventually paradigmatic concept of the prime form of classical set theory. Similarly, Janecek's more abstract notions of harmonic progression offer an interesting complement to those being promoted on the North American continent by Schoenberg (Structural Functions of Harmony) and Hindemith (The Craft of Musical Composition).
Yet given its orientations to developing mid-century philosophical and analytical directions, Janeček's work is uniquely situated at the heart of even larger and deeper intellectual directions in its continuous modeling of classical harmonic theory, its almost high-Medieval dedication to the sensory evaluation and description of harmonic quality, and a truly obsessive structuralism for exhaustive definition and categorization of theoretical schemata. Of these, it is perhaps the second, and most basic of these propensities of Janeček's work that bears the most promise to contemporary theoretical analysis. Indeed, one of the most striking consistencies of recent twentieth century atonal harmonic theory has been its neutrality to perceptual realities of harmonic formation, progression and processes of dissonance alternation, fluctuation, accrual, etc., perhaps in deference to the many abstract and even arbitrary compositional techniques for which it is so well adapted.
It has probably also not escaped the reader's attention that Janeček makes an impressive number of contentions and classifications of relevance not only to practical compositional pedagogy but to the study of music cognition. The distinctiveness, for example, of "increased" and "merged" dissonances and the similarity of chords within the dissonance maxima families, appear to make verifiable claims on our capacities of harmonic intuition. The perceptual reality of imaginary tones and their "cancellation" could similarly be explored as an aspect of short-term auditory memory and harmonic perception, and Janecek's differing criteria for ascending and descending whole-step cancellation seem to provide hypotheses about our perception of linear melodic continuity. Janeček's theory also bears clearly on our perception of harmonic complexity in its attribution of acute sensitivity to different dispositions of 313 structures and apparent indifference, in perceived dissonance, to different harmonic dispositions of 213 structures
In closing, an important interdisciplinary example can be taken from Janeček's later chapter on "Problems." Janeček makes no obvious attempt, despite the scope of many of his preambles, to provide a definitive and all-encompassing theory of harmonic structure. The concept of characteristic-maxima based on the association of dissonant elements was pursued to a point of complexity where it was clearly no longer operative and it was supplanted by its converse, a theory of triadic combination, itself with obvious limitations. The equal acceptance of bitonality and monotonal composite functions and even of functional and non-functional expressions of tonality itself (although Janeček is obviously much more interested in the former than the latter) further define his interest in the integral relationship of compositional and esthetic concerns to systematic theoretical insight. For Janeček theory and analysis take a clear stance at the intersection of the universal principal and the creative will:
Older music theorists strove to establish a binding and universally applicable system of compositional rules or norms. These efforts could not lead to a positive result, because they were futile. Living creation always broke through all elaborately constructed normative systems and worked its way to a new and a different compositional technique, ignoring theorists' rules. The impermanence of theoretical requirements and rules bears witness to the fact that their roots do not reach as deep as theorists might wish....Music theory takes universal law over from the natural sciences. It then creates artistic law based on artistic practice. Compositional practice tends to become stabilized for a time with certain idioms and procedures and, it is for music theory to capture, classify, and evaluate the essential practical gains so established.
....As long as universal law affects the attitude of practical artists, it must be reflected in the results of theoretical investigation. A precept that has been derived from practice can be more far-reaching and need not be merely an expression of temporary artistic custom. Thus it is an important task of music theory to define the role of universal law in practical artistic (technical) rules.
Appendix A: Janeček's Foundations of Modern Harmony Table of Contents


Appendix B: Commented List of the Examples in Chapter Twelve of Foundations of Modern Harmony
Paul Hindemith: In the String Trio op. 34, final movement, fugue, an essentially tonal melodic ostinato is set against intentionally harsh dispositions of the minor ninth.
Albert Roussel: In the op.45 String Quartet excerpts are taken from the slow movement and last movement. In the former a prolonged iiø6/5 before a closing cadence involving transient sonorities on theorder of dominant sevenths (see Example 35). More dissonant transient chords are seen in the final movement before a closing sonority defined more its repetitive insistence and preceding chromatic bass line than by its intervallic qualities.
Arthur Honneger: In Pacific231 the "locomotive" chords are taken as an example of an arbitrary dissonance structure within an obvious compositional repetitive sequential processes and extra-musical reference. In Prelude, Arioso, Fughetta sur le nom de BACH, a passages from the fughetta which presents a complex combined Lydian/Phrygian pre-tonic sonority harmonizing the "C" of the B-A-C-H motive at its final cadence
P Bokovec: The close of the Chorale in which the relatively "loose" functional motion is balanced by repetitive arrivals on the tonic. The beginning of the Wind Quintet presents a superposition of diatonic fragments in which strata-defining semitones and dissonant chordal cross sections are indicated.
Vítslav Novák:: A cadence from the Third Quartet provides an example of Janeček's adage of the effectiveness of a pre-tonic chord which has strong possibilities for resolution to a completely different tonic (see Example 36).
Isa Krejci: The Trio-Divertimento provides a further example of extended functional relationships to a C major tonic. In a somewhat difficult analysis Jane
ček characterizes the ambiguity of the opening as pertaining to either F# major, A major and possibly B major for which he gives a table relating the various functional degrees (DSPL) to the number of beats the pertinent degrees are heard. C major emerges based largely on the prominence of its dominant (second and third measures) and the relative weakness of its auxiliary functions. Janeček then concentrates on the passages where C major functions are clear amid apparently parenthetical passages of textural and chromatic complexity.(Example 37)Bouslav Martin: A short excerpt from the opera Julietta provides an example of intentional ambiguity where the tonic G minor is weakened by non-dominant linear motions and quasi modal progressions such as -D +S en route to D minor.
František Picha: In the Suite for String Orchestra and Gong the surprising B minor ending of the first movement is explored in a quasi-statistical manner, asserting a durational prominence of B minor (25 quarters) but in a relatively weak sense of the tonic in relation to G major which gives way via the D-S-S to B minor which is presented only in any degree of stability in the last four measures.

Example 35: Roussel: Closing Measures of the Slow Movement of String Quartet op. 45

Example 36: Vítslav Novák: Excerpt from Third String Quartet
© 1939 by Breitkopf und Härtel, Leipzig, used by permission

Example 37: Isa KrejčiTrio-Divertimento, Introduction
© Czech Radio
1. See "An Interview with Rudolf Komorous,"
ex tempore , III/2 (Fall/ Winter 1985-86), p. 57.2. In the original Czech: Základy moderni harmonie, Prague: 1965. At the point of completing this article, the translation of Foundations of Modern Harmony by Jana Skarecky and Anne Hall had yet to find a publisher. It is with their permission that passages from their translation are cited here.
3. From the original preface of the book entitled Modern Harmony. Although Janeček began this book in 1942 and finished it in 1949, important parts of the treatise were published in a variety of periodicals (Tempo and Rhythmus etc.) as early as 1931 and as late as 1947. Individual chapters of the treatise were revised and re published until the final version of the work was published as Foundations of Modern Harmony in 1965.
4.
See Appendix A which presents the table of contents for the entire treatise.
5. While in his preface Janeček distinguishes between his "imaginary tones" and the "pseudo-sensed"
(in the Skarecky-Hall translation) tones of Janá
Each of these nine combination possibilities can be illustrated by concrete examples of chord-types, of which we can study the sound and which we can compare with each other, evaluate, and characterize. This indispensable process, demanding detailed and intimate knowledge of the extensive material, knowledge supported by living practice, cannot be described here step by step.
7. Although by no means systematized, Janeček makes numerous interjections of a statistical nature from his unique perspective of chord types defined by dissonant elements. On the near omni-presence of the semitone he notes that it occurs in ten of the nineteen three-note chords, also in 10 of the 43 4-note chords but in only three of the 66 five-note chords, as presented in his charts in §25. Janeček thus hears the dissonant effect dominant seventh and half diminished sevenths sonorities as "softer and more integrated than that of the dull and unrefined minor-minor (seventh) chord." There is a potential confusion here which is never graphically resolved since 11 refers to both an orientation scheme for a three-note chord as well the semitone clash of semitones which arises from the four-note orientation scheme 111.
10. The hyphen which does not appear in the Skarecky-Hall translation, is intended here to alleviate the potential English-language confusion of "characteristic" as a noun and "characteristic" as an adjective.
11. Janeček obviously does not subscribe to the adage of the origin of the half-diminished and diminished seventh chords in rootless dominant major or minor ninth sonorities. We might also assume problematically from Janeček's discussion that the dominant seventh (GBDF), the minor-minor seventh, GBDF, the augmented-minor seventh, GBD#F, and the flat-fifth dominant seventh, GBDF, are quite different classical "harmonies" of which the chords G-B-F or G-D-F would represent various ambiguously incomplete forms.
12. Once again from his charts in §25. Janeček acknowledges Leos Janáček's as having coined this term. Janeček also provides graphs for the subgrouping of each maxima family. The subgrouping of maxima and nuclei family for 2 is represented in chart form as the following:

where, as in his orientation schemes for 3-, 4-, 5-, and 6-note chords, the bracketed numbers refer to the octave complement interval.
15. To a certain extent, the inventory of dissonance maxima has already been introduced in the preceding exploration of unmerged (i.e. increased) dissonance elements. In this chapter the maxima of merged dissonance elements as well as those containing the tritone and semitone clashes (11 and 66) are added. More specifically Šin's theory combines functions of Tonic, Dominant, Subdominant, which Janeček extends to the Phrigian and Lydian. While these latter functions are not observed in Janeček's triadic combinations, they are later applied his analysis of chord progressions.
17. Janeček's designation of "combination" and "non-combination" is somewhat counter-intuitive since the former refers to a registral separation of the two triads and the latter to combined mixing of the two triads or triadic elements. The issue of Janeček's "imaginary tones" is probably worthy of a study in itself in the broader context of tonal coherence. Janeček makes no attempt to find (Schenkerian) layerings of voices over the broader cancellations of harmonic tones and he similarly does not seem to recognize such phenomena as cross-registral voice-leadings. Janeček differentiates here between the voice-leading of classical harmony and mere pitch succession which applies independently of the part motion. Dissonant chords are excluded as pre-tonic chords since the essence of a functional relation for Janeček's is that "the substantial characteristic of gravitating to the tonic is separate from inner sonic tension." In other words the pre-tonic chord must be a pure "extract freed from the secondary characteristic of real dissonance." The superscript or subscript represents the root of the inter-function chord in number of semitones above or below the tonic. With the annotation that the progression DS (Dominant to Subdominant and its derivations) is historically avoided as unnatural but its opposite, SD, is common and completely natural.
23. The dots in the example show the completeness of the functional degrees (two dots to the right of the function symbol indicating the presence of two of the three tones of the triad) as well as the seventh (the dot above the functional symbol) and any added tertian elements (the horizontal dots above the tertian symbol). Altered tones in any of these sonorities are indicated via commas instead of the dots. Thirds added below the root of a function are indicated by dots (usually one or at most two) beneath the function symbol. The symbol (d) is used for an applied minor dominant. The brackets indicate the function of the chords as applied subdominants and the small (s) for the D minor sonority represents the fact that it is a minor, and hence altered subdominant in A major. Janeček actually recognizes three case:s "music in which the meaning of the chords is definite and unambiguous, (b) music in which the functional relations are loosened, and (c) music in which no functional relations between chords can be objectively and reliably determined." As noted in the Skarecky-Hall translation, "styling" is their term for stylizace which is more literally rendered as "stylization" or "conventionalization".
28. F.Z. Skuherský, Theory of Harmony with Scientific Foundations in its Simplest Form 1885.