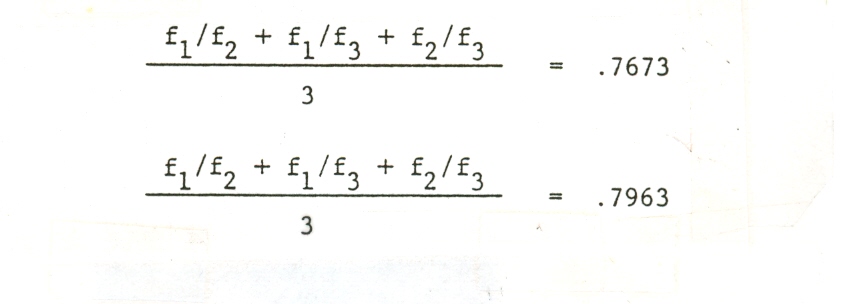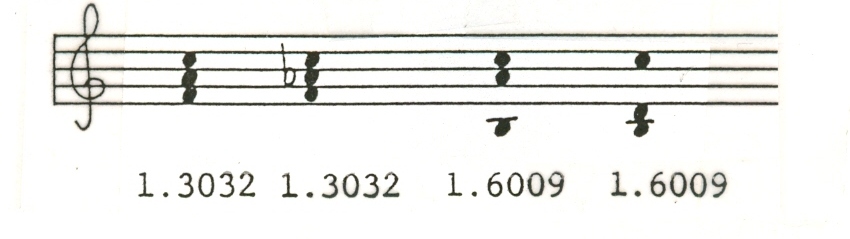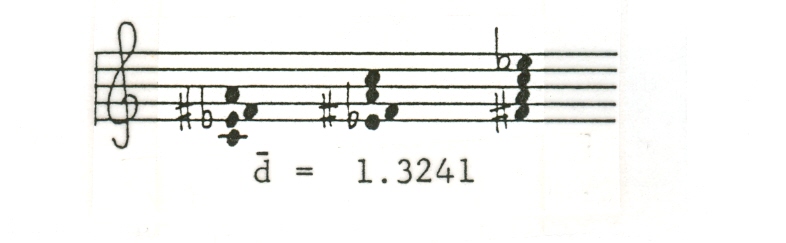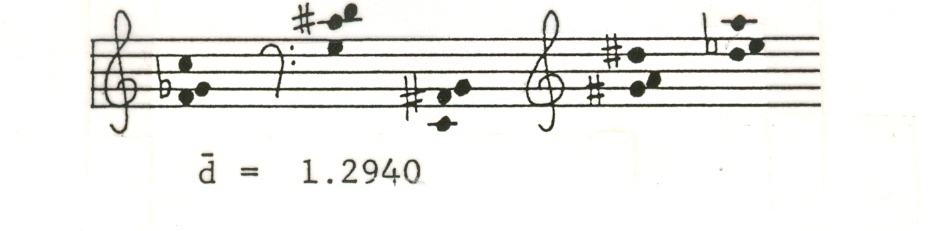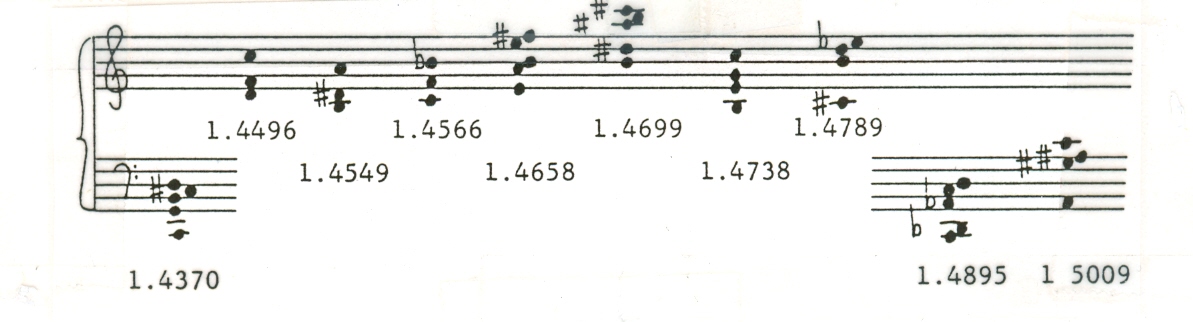Density in a Musical Context1
E.
Michael Harrington
Part One
The following essay
will outline this writers attempts at defining density in music, deriving quantitative measurements of density, and
using all such information in an
analytical and compositional manner. A comprehensive definition and assessment
of density, one that will exemplify the interdependence of all of the
musical parameters, i.e., pitch compression,
range, distribution, dynamics, instrumentation, etc., in a numerical representation, is impossible.
Limitations have been imposed from the outset.
This discussion of density will discount the
effect of instrumentation upon the sound (i.e.,
for this paper, how the sound is produced is not of concern to the measurement). Secondly, dynamics will not be of importance in assessing density. The amplitude of a pitch will have no bearing whatsoever upon the density. Lastly, time will not be considered essential in density analysis. It is at this point that I differ most
from others who have dealt with density in
either a compositional or analytical manner. lannis Xenakis, for example, measures density and
utilizes it as a function of time (i.e., the
number of attacks/events per unit time). The vertical or concurrent aspects of density (e.g., a chord), are
not of the same paramount importance
in the compositional process as they are to this writer. Xenakis derives
his vertical structures in procedures which are only incidental to
considerations of density. Wallace Berry, on the other hand, attempts to
measure density in both the concurrent aspect as well as in the linear unfolding and accrual or decrease in the
number of parts present in the musical texture. His numerical representations
of vertical density (and linear
density) fail to differentiate between degrees of consonance or dissonance, the spacing of the chord, the effect of
mirror inversion, the register of the
event, the effect of transposition upon the chord, and the use of the
same intervals in a different order (i.e., permutational
variations).
Density, I feel, is a parameter capable of being precisely defined through
an accurate and logical means of analysis. Conditional statements regarding analysis of
vertical texture in the past have been of a general
nature with a minimal distinction afforded between sonorities considerably from each other. For example, it is
not enough to state that a chord is a
four-note event, or a five-note event, as aspects of register, compression,
and chordal quality are not taken into account.
Consider the four-note chords below (Example 1). They are
obviously representative of disparate constructional
features and share in common only the fact that they are all
four-voice sonorities. It is clear that the number of voices present in the
simultaneity may mean little, if anything, in analysis.

Example 1
An account of pitch-range compression in analysis will yield
a more precise description of the chord. For
example, the first chord's four elements are distributed over a range of
1512, chord #2 over 1161, chord #3 over
1521, and chord #4 over 1211. A convenient nomenclature for such a density
representation is shown in Example 2.
#1 #2 #3 #4
4:5 4:16 4:52 4:21
Example 2
This
quantitative device is used by Wallace Berry and is described in his book
Structural Functions of Music.3 Or,
two types of fractions can be determined - one that will yield indexes larger than 1, or
the reciprocal function which will result in
numbers smaller than 1, but greater than zero4 (Example 3).
4/5 = 0.80 4/16 =
0.25 4/52 = 0.08 4/21 = 0.19
5/4 = 1.25 16/4 = 4.00 52/4 = 13.00 21/4 = 5.25
Example 3
The fault of
this system lies in the fact that it does not represent a special-case chord, but rather a myriad of chords.
To illustrate this weakness, the following example is offered. Constansinarcseccot,
by this composer, consists of six chords repeated in
various guises. All of the chords are
four-voiced and span a 1161,
yet this system of density cognition fails to differentiate
them (Example 4).

Example 4
Part Two of this paper will attempt solutions to these and other
problems. All subsequent definitions of density will involve
calculations and treatment of equally-tempered intervals only, and
assessment of vertical pitch structures regardless of time
consideration, amplitude, and instrumentation, but necessarily involving register,
spacing, range, consonance/dissonance level, and pitch-compression.
Part Two
In a vertical structure, frequencies are
sounding simultaneously in ratios to one another. The relationships
contained within a chord, the sum of the frequencies in vibration,
are analogous to the number of
relationships in a star event5 The number of interval relationships
which must be assessed in a chord is determined by squaring the
number of pitches,
subtracting n from this number, and dividing by 2.
(n2 - n)/2 All Self-contained interval relations
n = the number of notes present in the chord
A
brief table of sonorities of increasing voices, and their total number of
self-contained interval relations (star events), follows in Table 1.
Notes in sonority
Total
interval relations
2
1
3 3
4 6
5
10
6
15
7
21
8
28
9
36
10
45
11
55
12
66
.
.
.
.
88
3828
Table 1
In assessing density, then, more
calculations will be involved for a larger chord than for a chord
with fewer notes. Because the chord exhibits this number of relationships, which is necessarily more than the
number of notes in the chord (unless the chord is of three notes, or
a two-note dyad), it is of extreme importance to consider
all such elements, as subsequent discussion will prove. In other words,
non-adjacency of pitches in a sonority accounts as an integral part of composite analysis.
We are now ready to invoke an operation
on the chord which will account for all the relationships. We
begin with the division of each frequency by all of the frequencies
above it (i.e., higher frequencies are divided into
lower frequencies, obtaining numbers less than one). All of the
derived quotients are then added together and divided by the number of
interval relationships in the sonority to achieve a mean. Symbollically,
the equation
can be stated as shown in Example 5.
n-1
n
1
/ (
∑
.
∑
. fj / fi )
/s = d
j=1 i=j+1
fn-1
is the second highest frequency
fn
is the highest frequency
S
is the number of interval relations (star events)
Example 5
To consider some
chords, we arrive at the indexes shown in Example 6.


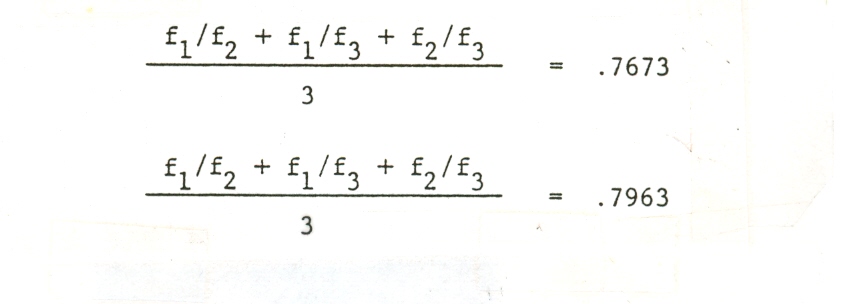
Example 6
The density index, at
this point, is inverted to yield a number larger than one, and, in fact, larger
than 1.0595; the interval of the half-step. The two indexes for Example 6
should be revised - 1.3032 and 1.2558 respectively. More chords and mean
densities are shown in Example 7.


Example 7
The
measurement of density is such that the chords which span the greatest distance will have a higher index.
Conversely, those chords which span a
closer, narrow distance, will have a lower index. Two
pitches a half-step apart will be
1.0595 according to this index. This is the twelfth root of two and will be the lowest number assigned
to a vertical entity because it is
the closest possible positioning afforded by equal temperament. Four-note sonorities, which always
contain six consequential intervals,
will reveal similar features with respect to changing areas of musical
space (Example 8).
Example 8
Because the same ratio occurs between each half step, chords
with identical spacing will exhibit the same
index of density,
d, regardless
of registral placement.
For example, the major triad made up of the contiguous
intervals 141 and 131, will have the same density index in any octave in which it
appears (Example 9).

Example 9
So
far, the chords to which we have ascribed an index corresponded to an auditory
experience (i.e., as the range of the three- or four-note chord increased, the numerical representation grew larger, accordingly).
And as the chord became more compact, so also did the representative index decrease, reflecting the diminishing area of
musical space covered by the chord. What would be the effect, both
auditory and analytical, of altering a simple
triad by introducing pitches within its extremes (i.e., by changing a three-note chord to a four-or five-note
chord of the same intervallic span) (Example 10)?

Example
10
It can be seen from this example what
the effect is of this outside-oftime parameter, i.e., the perfect fifth
between outermost voices being internally modified. It reveals the same feature as the
widely-spaced chord which undergoes a
uniformly spatial reduction (i.e., as the pitch compression increases, and/or the overall range decreases, the density index
decreases).
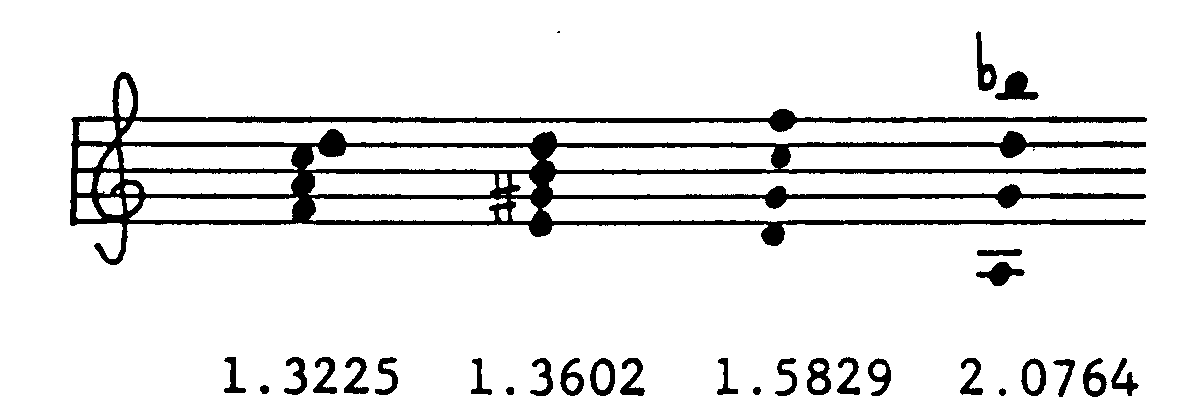
What
is the effect of interval order permutation upon contiguous intervals
of a sonority? For example, would a similarly-voiced
major and minor
triad have the same density? (Example 11)
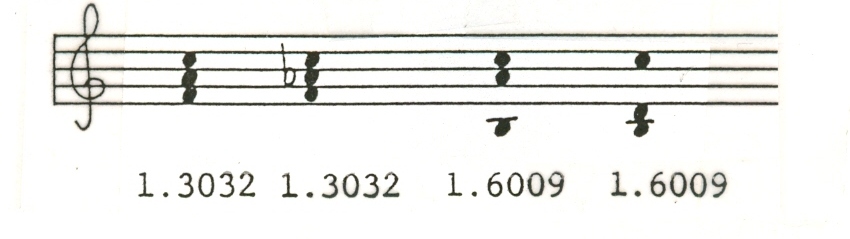
Example 11
Reversal of contiguous
intervals has no effect upon three-note chords. In a larger chord (i.e., one with more members), will mean densities change when the intervals in a sonority are similarly
rearranged? And what is the effect of such dispersion (i.e., permutation
through adjacent element order rotation)? If a chord consists of n equal
intervals, such as a diminished 7th chord
arranged in a series of minor thirds, the density index will be constant provided that the equal interval
disposition is never violated (Example 12).
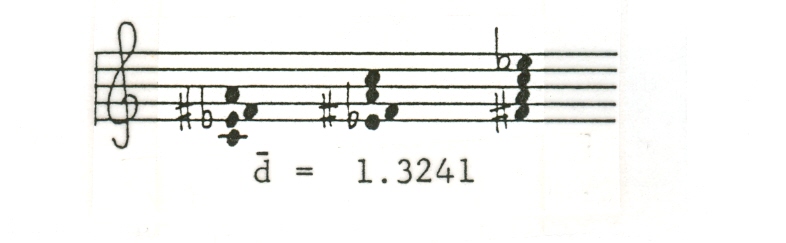
Example 12
This
was realized in the prior analysis of a major chord where the intervallic
unity was maintained within various registral
contexts. However, will the density index be the same if the pitches
within the equal interval chord are dispersed over an enlarged
area? Let us examine such a revoicing as a case in point
(Example 13).

Example 13
The index increases as the pitch compass increases, as was made evident in
the earlier inspection of pitch ambitus effect and
function. Now, if the three contiguous intervals within the
four-note diminished 7th chord are arranged in a different order (yet maintaining
the same span of musical space) from a vertical concurrence of
[6], [3], [6] to [3] [6], [6], and [6], [6], [3], will the density index
remain constant (Example 14)?

Example 14
This proves that the same intervals rearranged, as in a permutational series, will result in different
indexes as well as different quality chords. It further
demonstrates that not only must contiguous intervals, but all combinations
of the interval events, be calculated, for only in assessing every event do the
real analytical, perceptual, and structural differences manifest themselves.
Because of this system's equal treatment of registral location and transposition
of an entity, the same density index can represent chords of various guises and locations in musical space. Whether this flexibility of chordal quality, placement, and function stacks up to our perceptual experience on an absolute scale may be irrelevant,
especially if the desire is for the
compositional generation of a diverse musical system.
The
following chords are of a 1.2940 d (Example 15).
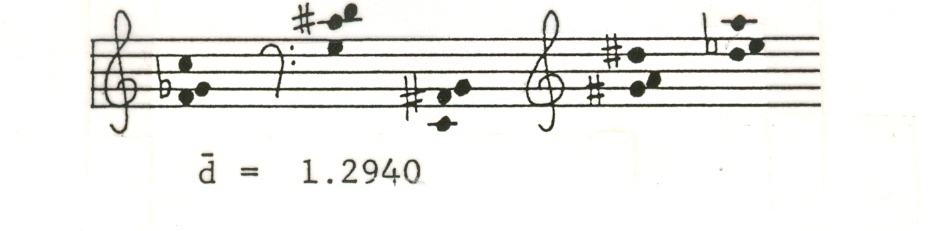
Example 15
Only
one calculation was necessary for the generation of such a
series, for the consequent chords are
merely transpositions and permutations of the initial chord's contiguous elements.
If intervallic identity is exactly
preserved, the chord may appear in any register and maintain the same a. The following chords (Example 16), exhibit a slightly increasing a between adjacencies.
The enormous variety of voicings
and registrations attainable through use of this system is of utmost compositional importance. The system can be made as
imaginative or as restrictive as the individual composer desires.
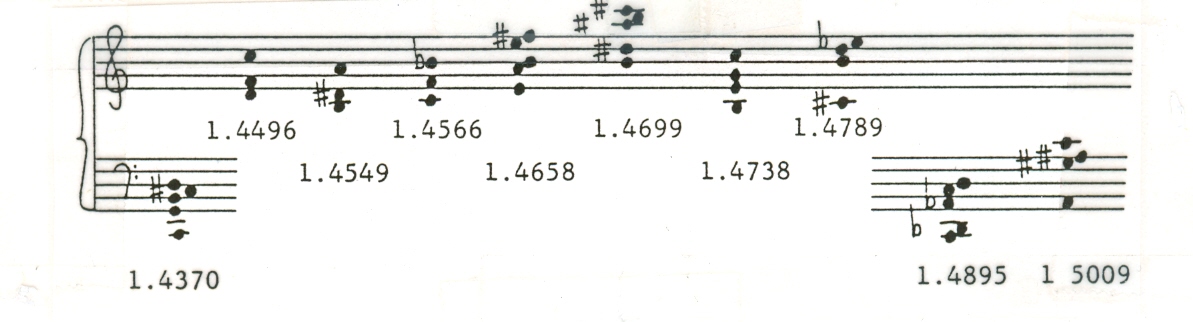
Example 16
There
are other possible ways to measure density. For example, in the previous equation,
the number of notes within each sonority was not necessarily reflected in the density index. A
four-note chord could have a higher
or lower index than some 2-, 3-, 5-, 6-, or 7-note sonority. An equation which will immediately reflect the number
of notes within the sonority (i.e.,
the weight) has been developed, and is illustrated in Example 17.
n-1 n
1 / (
∑
.
∑ .
fj / fi )
/s + number of notes
= d
j=1 i=j+1
in chords
Example 17
The new equation,
da,
is similar to the initial measurement,
d. To derive
da, the initial equation a
is
performed, to which, the number of notes in the sonority is added. In Example 18, the differences between the two systems
are as striking as the conclusions drawn from the two systems.

Example 18
When using
d, as the number of notes in
a sonority increases (i.e., the weight increases), the density
index becomes smaller. However, when using
da, as the number of
notes in a sonority increases, the index becomes enlarged to reflect this change. Because the original
process, a, is intrinsic to, and subsumed within
da,
interchangeability between indexes is very simply achieved:
d to
da involves one addition;
da to
d involves one
subtraction.
If we are now to re-evaluate the music
of Example 16 according to this new process,
da, we will have a different nexus of density. As Example 16 was delineated
according to a gradually increasing
d, so now is it reordered to
exemplify an increasing
da value between successive simultaneities. The
two systems are compared and evaluated in Example 19.

Example 19
The nature of the interval calculations of
d is preserved in the
da process - chords containing the same
number of elements will constitute the same hierarchical order using
da as they did when calculated simply by
d.
The effect of the constant in the process is not significant when dealing
with a uniform element-number family (Example 20).
da is very similar to
d in that the measurement of the density
of a sonority will be the same in any registser, provided that intervallic
identity be strictly preserved. (Example 21).

Example 20

Example 21
A simpler method may be devised that will account for the
number of notes in the sonority - it will
reflect the function of increased or decreased weight in the sonority,
as did
da. The two previously discussed methods of calculation,
d and
da, encompassed every conceivable
interval relationship within the sonority.
As was illustrated in Table 1, the amount of star events in a
sonority grows larger, necessitating many calculations. For the composer who wishes to attain a density index for chords of a very large size, and
does not have the use of a computer to quickly perform the frequency calculations, an easier system is
needed. The system will not concern
itself with star events, but instead will develop its representative value
through a summation of frequencies in the chord. The frequencies are added together, the logarithm of the frequency
sum is taken (to reduce the values to
a range comparable to the previous indexes), and the number of notes in
the chord are then added to this number (Example 22).
n
log
(f
∑
) + n =
db
n-1
Example 22
To appreciate the
practicality of such an equation, one need only consider the number
of events which need not be regarded in subsequent calculations. For example,
in an eight-note chord, using a or
da, 28 intervals must be calculated. Using
db, as we will designate it,
only eight intervals have to be added. A 20-note
chord would necessitate 190 calculations in
d or
da; only 20 with
db. Its operational
simplicity is of paramount importance.
In comparing the following chords
(Example 23), all triadic with a diminishing span, a decreasing index of density occurs as a
result of this summation process (db), as it did in the initial measurements (d
and
da). This
system does, however, distinguish between major and minor chords of the same span.


Example 23
Using the initial
density index,
d,
the lowest possible value is 1.0595. Are we to surmise from the minor second in the
previous example that 5.8569 is the minimum possible value in the db
scale? This is not so because we are
dealing with an arithmetic, linear process, and accordingly,
higher pitch groups will have higher indexes than
transpositionally equivalent
lower pitch groups. The minimum and maximum values for half-steps are
listed in Example 24.

Example 24
This system,
then, differs drastically from the previous systems in its treatment of
registral placement. The system considers register and instrinsic
entity in the analysis of density. The
system does not respect equal-interval sonority transposition as did the
other systems (i.e., a sonority will undergo a density modulation as its
placement in musical space changes) (Example 25).

Example 25
The
chordal series of Example 26 and 27 represent half of the possible permutations
of the interval series [1], [2], [4] [7], which occur in
the first chord. These chords are now
arranged in a specific order - from lowest to highest - according to an inverse mean
frequency ratio,
d.

Example 26

Example 27
If the system is then
analyzed according to
db
and again
arranged in increasing values, a different
ordering will necessarily result. This is, of course, due to the
inherent differences of the disparate systems involved (Example 28).

Example 28
The four-voice sonorities from Example
1 can now be analyzed according to these various equations.
The indexes will necessarily differ due to the disparate
considerations of logic and the various definitions ascribed to density (Example 29).

Example 29
Through the use of these density indexes, one can choose to define density by the following
means: independent of registral location (d,
da); independent of the
number of elements contained in the sonority (d); being the result of only its contiguous pitch relations
(db); or being independent of consonance/dissonance considerations (db).
1 A
paper presented at the American Society
of University Composers XIV National Conference at
the
University of California, San Diego, March 14, 1979.
2 Intervals will often be referred to by the number of halfsteps within their span, e.g., 1121 is an octave, 171 is a perfect fifth,
141 is a major third, etc.
3 Wallace Berry, Structural Functions of Music, Prentice-Hall,
Inc., Englewood Cliffs, NJ, 1976.
4 Sole
exception occurring in the case where contiguous minor seconds occur and the
numerator and denominator exist in an n- 1/n or n/n-1 relationship.
5 Star events is
the term used to define relationships
between n events taken two at a time. R. Buckminster Fuller, Synergetics, MacMillan Publishing
Co., Inc., New York, 1975, p. 60.