Dialectic in Miniature:
Arnold Schoenberg’s Sechs Kleine Klavierstücke Opus 19
Matthew
Greenbaum
If one were to ask, “is there a
principle of contrast in Schoenberg’s music?” the answer, while always affirmative,
would vary, depending on where a particular work fell in the chronology of his
compositions. While the 12-tone works demand a certain set of answers to this
question, Schoenberg’s transitional works - those that precede the twelve-tone
system and follow the more-or-less tonal works - offer varied examples of
dialectical processes.[1]
The collection of miniatures, the Sechs Kleine Klavierstücke Opus 19, is
an interwoven fabric of tonal artifacts and there are distinctions between the
horizontal and vertical aspects that reveal a subtle connection to the tonal
universe. What these aspects have in
common is a high degree of symmetry. In the conflict between these aspects lies
the dialectical process that governs the work as a whole and the six pieces
individually.
The musical concentration of these
pieces - combined with their brevity -creates a highly ambiguous musical
language that defies conclusive analysis. Indeed, it is one of the attractions
of Opus 19 that the longer one studies it, the more heterodox it seems.
The concept of symmetry as an
organizing structural principle was not Schoenberg’s invention. Toward the end
of the 19th century the idea of the tonal center became entwined with notions
of inversional balance. The influential Hegelian music theorist, Moritz
Hauptmann, provoked a re-evaluation of musical structure when he analyzed the
tonic/subdominant relationship as an inversion of the tonic/dominant; David
Lewin links this to Schoenberg’s tonal and post tonal practice, illustrating
similar structures of inversion in the First
String Quartet and the cruciform symmetries of Pierrot Lunaire.[2]
The
symmetrical implications of Opus 19 have been studied by Jonathan Dunsby and
Arnold Whittall, who attempt to explain the second and sixth pieces as total
symmetries, akin to the first movement of Anton Webern’s Symphony Opus 21. This requires a certain amount of manipulation;
Dunsby and Whittall sometimes fill in incomplete symmetries with pitches that
appear later in the pieces and certain octave displacements are necessary.[4] Although their Example 29, an analysis of the
second piece of Opus 19, shows tightly packed chromatic regions toward the
center and relatively larger intervals at the extremes, similar results might
well be attained from many chromatic pieces, given the general tendency toward
larger intervals in the lower registers, and saturation of those intervals
within the treble and bass staves.
Even within the confines of tonal
music Schoenberg recognized a motivic kinship between like intervals (i.e.,
symmetries) in musical development. In Fundamentals
of Musical Composition he writes: “Every element or feature of a motive or
phrase must be considered to be a motive if it is treated as such, i.e., if it
is repeated with or without variation;” [6]
he also notes that dyads can be motivic details, or any “pitch succession or
duration succession of two or three members …”[7]
This is significant when one considers the multitude of dyadic symmetries in
Opus 19.
In Opus 19
the interval sound - its Klang - is
tied up with replication of like intervals. Focus on the actual sound of a
pitch rather than its relative meaning within a tonal structure was a decisive
step in Schoenberg’s musical evolution.
The often-noted 05s (perfect fourths) in the opening of the Kammersinfonie Opus 9 are a familiar
example, and perfect fourths play an important structural role in Opus 19 as
well.[10]
Indeed the Kammersinfonie opening
foreshadows a texture completely dominated by this one interval (end of measure
360 to 368; end of 371 to first half of 373). Such a concentration on a single
interval is probably the first appearance of such an idea in the history of
music.[11]
The whole-tone content of the first theme of the Kammersinfonie is similarly composed out (Schoenberg was proud of
the work’s integration of themes and harmonies).[12] By Opus 19 the interval was liberated and was
projected into the free musical space of which Edgard Varèse and Stefan Wolpe
would later speak.[13]
The
differentiated function of steps and skips in Opus 19 is a relic of tonality.
From the perspective of Schoenberg’s twelve-tone works, which banished the
distinction between the horizontal and vertical, it seems out of character to
find just such a distinction in Schoenberg’s earlier music. And yet, verticals
are manifested in Opus 19 by specific intervals deployed in symmetrical
configurations: in the entire six pieces there are no simultaneous pairs of adjacent half steps or whole steps - or pairs
of adjacent half-steps and adjacent whole-steps; these interval combinations
are always expressed horizontally.
Adjacent half
steps often act as connectors between symmetrical events, recalling similar
moments in Debussy’s Des pas sur la neige.[14] The dialectic between the vertical skip
and the horizontal step, long present in Western music - where ”Pythagorean”
perfect intervals oppose the melodic line and its dissonances - is still
faintly present in Opus 19. One can think of symmetrical simultaneities as
points of relative stasis and of steps as destabilizing transitions. Melodic
shapes - particularly in I, III, IV and V - can be heard as surface
manifestations of the interplay of symmetries.[15]
The following
analysis is based on an Occam’s razor approach; it considers only two elements:
like-interval sets (3/3, 4/4, 5/5, etc.) and horizontal symmetries. While
possessing no specific tonal function in the work, like-interval sets appear
throughout, sometimes alone and often interpenetrating. Horizontal symmetries, in contrast, form
connective links between these cells.
The 3/3/3, “diminished seventh,” and 4/4, the
“augmented triad” cells, have a special property not shared by sets other than
the total chromatic: they are infinitely repeating (i.e., C E
F# A/C E
……/C E G# C E …..). Besides its
philosophical suggestiveness, this property helps to form the specific Klang of the work; these subsets are
more “redundant” than other subsets: their registral displacement merely
produces more of the same pitches, forming a subtle timbral backdrop less
determined by registral distinctions than the asymmetrical elements that create
the specific environment of tonal music. The frequent 5/5 details imply a
fourth cycle which would require 11 iterations to return to its initial pitch
class, like the chromatic scale. However, it is still an infinite series, and
to the extent that it plays a role in the piece (particularly in pieces I and
VI) it also suggests boundlessness; indeed, the quartal, ic5 collection, which
fully emerges only in the last movement, is prepared from the first measure of
the work, as will be discussed in relation to piece VI.
Every pitch
in Opus 19 can be understood as a member of at least one symmetry, although
nearly all pitches are members of at least two. Besides the like-interval cells
and linear symmetries, there are contour symmetries and convergence symmetries,
which will be discussed below.[16]
A special chart is devoted to the emergence of ic5 symmetry over the course of
the pieces.
In the
following analyses, the four possible augmented triads are indicated as AUG0, 1, 2, 3 (G B D# = AUG0 as in measure 1 of I, see Example
1 below). The three diminished seventh
chords are identified as DIM0, 1, 2,
where DIM0 =A C D# F#. Diminished
triads are included in the DIM forms
to which they belong. Other symmetries are bracketed and expressed as interval
pairs, with additional interval projections indicated as well. AUGs and DIMs in which a symmetry is disturbed by registral displacement are
indicated with a slash line through the circle indicating the symmetry.
Consecutive
symmetries in Opus 19 often share a common tone.[17]
Their combination and linkage determine the narrative of each piece. To
whatever degree the pitch-class content is subset-related, these relationships
are of a lower order of structural importance than registral symmetries.
Schoenberg, in the radio address
quoted above, notes that “a minor third can become a major third.” If the remark has any meaning - and I think it is very significant - it must
refer to such events as the opening right hand collection in the first piece B
D# F F#, compared to the subsequent B A F# D#
in measure 2. Or, in measure 3 the converging figure B E A G G# (-7 +5 -2 +1).[18]
Since the pieces are composed of ic3 and ic4 compounds, the entirety of the
work can be heard as a play of expansion and contraction, signaled on the
larger scale by convergent figures such as the one in measure 3.
Scalar
Motion
Series of whole
and half steps form connections between harmonic events throughout the
opus. In piece I, the chromatic descent
from the F in measure 4 down to the A at the end of measure 5 foreshadows the
major third descent at the end of piece
II, the linear ascent and descent in piece III, measures 1 to 4 (lh), and the
stepwise ascent in IV, measures 4 to
6 and 7-8. Note that the chromatic descent in I is also clearly referenced in
IV, measures 2-3; both begin with an F in the same register:
I: F (G) E E-flat D D C
B B A
IV: F
E D# D (C# preceding F) C A# B
Figure 1:
Comparison of Scalar Motions in Piece I, m. 4 and IV m. 2-3 in Op. 19
Linear Symmetries
Symmetrical step-wise motion permeates Opus
19. Note, for example, in I m. 6 - 7 (lh) the dyad pair D E/B
A (+1 -1). It connects the AUG2 in measure 6 with the DIM2 in measure 7, or the -5/+5
symmetry between measures 16 and 17 (lh). This ic5 cell recalls the D
and F# in measure 2, where they occur in the same register:
Measure
2: rh
A B / lh F
E D B
Measures
16-17: lh B A E (rh)
F# C# F
Figure 2:
Comparison of Scalar Motions in I, m. 4 and I. m. 4-6, 7-8 of Op. 19
Convergence
Convergent motion
- a pattern of decreasing interval sizes - is a most interesting surface detail
in Opus 19; it is essentially highly developed contrary motion and often in the
form of a compound melody. It occurs a number of times in I (see Example 1 below): the first across
measures 2 and 3, fills in a minor third, the second is in measure 3 and can be
understood either as a strand of shrinking interval sizes or as contrary motion
by steps (B-A-A / E-G-G#). A third, in
measure 7, is very close to conventional voice leading, and the convergence in
measure 13 (lh) answers measure 7 and extends into the next measure. The very
significant convergence at measure 11 is echoed in another prominent
convergence in V, measures 1 to 3. The cadence point - F# D# E - is common to
both figures. Secondly, the passages
share the same pitches:
I measure 11 rh: D/B F G (C#) F# D# E
V
measure 1 lh: D F G (B) rh: F# D# E
C.f.
III m. 7: D# E
Figure 3:
Comparison of Convergent Motions in I, m. 11 and V m. 1, of Op. 19
Finally,
as we shall see, convergence in the final measure of I is of crucial importance
in the unity of the work.
Contour
Symmetries
Contour
symmetries, i.e., brief arch-forms, are ubiquitous in the six pieces (indicated
by V-shaped lines). These brief oscillatory moments are a bit nostalgic -
similar shapes might occur in Schumann - but they also reinforce the
thoroughgoing symmetrical structure of the work. While contour symmetries occur
earlier in the first piece - e.g., measure 2 A B
A - the most prominent is the concluding gesture, which foreshadows events in
subsequent movements and signals closure in the first piece. The uppermost
contour symmetry D# E D# is a very significant foreshadowing of the last piece.
Opus
19, I
The first
piece in the Opus 19 collection is very suggestive of a prelude: it is the
longest of the pieces and most varied in texture. The arpeggiations in the first
three measures signal its prelude quality, while the melodic arc of the first
two measures is a model for both the conclusion of the movement and for similar
melodic shapes in the others.[19]
The
sudden intricacy of measures 4-6 is governed by a descending chromatic line
(discussed below), supported by a series of AUG and DIM cells and
concluding with the contrapuntal
measure 6. A second melodic arc can be
traced in the left hand of measure 6,
passing to the
right hand A in
measure 9, then t o the
G in measure 10, and finally converging on the E in measure
12. This shape encapsulates the movement’s emergent moment - the
tremolo/sustained figure in measures 8-12 - and connects it with the
contrapuntal music. Two further melodic arcs (13-14, 15-end) close the
movement, in a gently lingering decay anticipating the conclusion of the entire
set.
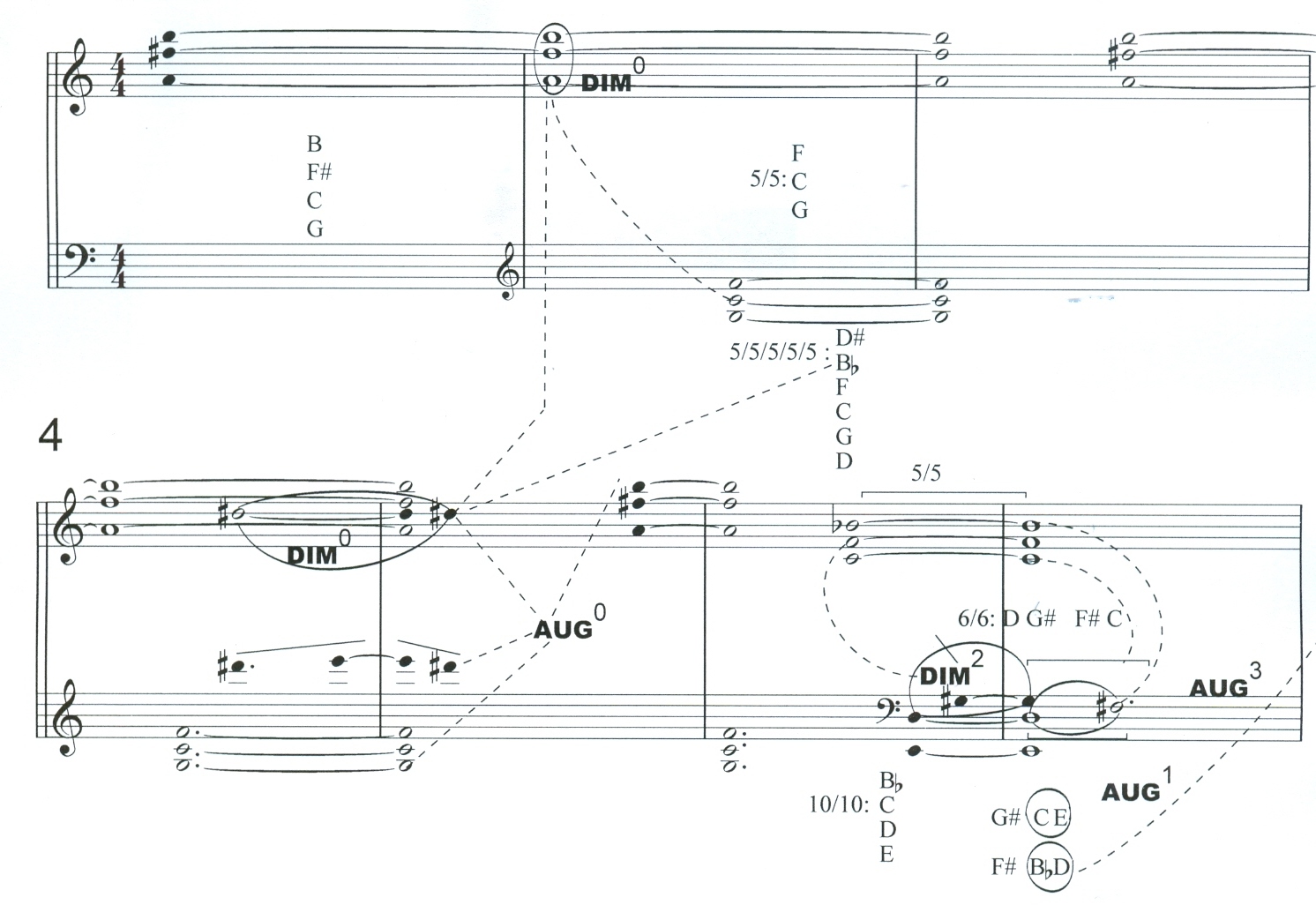
Example 1: Schoenberg,
Sechs Kleine Klavierstücke, I
All
transpositions of the third-cells are exposed by measure 5, which concludes
with an unadorned first statement of AUG3,
a cell that also occurs in the last measure. AUG0 has cadential implications in three of the other pieces as
well:
First Measures Last Measure
I AUG0 AUG0
I AUG0 AUG0
III AUG0 AUG0
IV
AUG0
(penultimate measure)
Figure 4: Use of
Opening and Closing AUG0 Collections
in Op. 19
In addition,
nearly every pairing of third-cells in the entire set first appears in this
movement. As noted above, the DIM0
and AUG0 in measures 8 to 10 are
first paired in measure 1. These pairings - often, interweaving - create the
quicksilver harmonic interplay so characteristic of this movement.
The AUG0 tremolo/sustained figure in
measures 9 to 13 is the longest event in I, and its emergence is carefully
prepared in the opening measure where this trichord first occurs together with
the DIM0 collection (notes G and B
appear in the same registers in both places). The tremolo/sustained figure
decelerates the harmonic motion, but its bonding with the mercurial events
accompanying it assert the dialectic of vertical and horizontal symmetry.
Measure 2 of
I contains a brief but significant contrapuntal moment: the superimposed
imitation of B
A F# D# and F E D
B.
Measures 4-6 present a dense web of contour- and inversional symmetries linked
with the chromatic thread running through the upper voices. Symmetries are
formalized by inversion in measures 5-6:
measure
5-6: A G B/D F#
F
measure
6: D F# F/E D# G
Figure 5:
Contrapuntal Symmetries in mm. 5-6 o op.19, I
These
measures also contain less formally related cells, such as the A A C# in the inner voice of measure 6 and the lowest voice F D E,
both comprised of thirds and half-steps.
The form of
each piece is to a great degree determined by the location of its cells. AUG0 is of particular importance in
piece I and throughout the set, especially its pairing with DIM0, as in I mm. 1, 4 and 9. In measure 4, the pairing precedes the
semi-cadential AUG3; in measure 8
the pair makes up the “emergent moment.” In the final measure, a brief AUG0 is encapsulated in AUG3, which now forms a full cadence
(in phrasing rather than tonality), as opposed to its earlier half-cadence.
Opus
19, II
Opus 19 II is
a study of ic3 and ic4, placed in various symmetrical relationships with each
other and underpinned by broken linear patterns. There are no ic5s or ic7s in
the movement.[20]
The obsessive concentration on ic3 and ic4 is signaled by the B/G ostinato
figure that runs throughout. Following the diminished triad “half-cadence” in
m. 6, the conflict between major and minor thirds is resolved definitively in
the last measure in favor of ic4 with the superimposition of two augmented
triads.
In contrast
to the orderly situation of ic4s in specific registers, ic3s are rather “vagrant”
(to use Schoenberg’s anthropomorphism). The dyad D#/C, first occurring within
measure 3, appears an octave higher as an interpolation in the B/G ostinato. It
reappears as a simultaneity in its original register in measure 6 as one of a
pair of such repetitions, the other being C/A,
also in its original register. The reappearance of these dyads opposes the
third-types: a pair of ic4s (C/A,
C#/A) is succeeded by a pair of ic3s (E/C,
D/B). The F#/D# ic3 between measures 2
and 3 appears an octave higher between the two augmented triads in the final
chord, encapsulating the interval in a dialectical end point.
Particularly
noteworthy is the “half cadence” of superimposed diminished triads at the end
of measure 6, and their “resolution” in the concluding superimposed augmented
triads.[21]
The diminished-triad verticality is an adumbration of a similar event in the
previous measure in which DIM0 and DIM1 are superimposed, with the G out of place.
The ostinato
B/G that runs through the movement is symmetrically completed by the E
B G triad in the final chord, and foreshadowed at measure 4. Similarly, the
upper triad of the final chord - D B
F# - is foreshadowed by the B/G
in measure 5 and the high D in measure 2.
The descending
line of whole steps (measures 7 to end) is unique in the opus, although echoed
in V, measures 8-10. Harder to parse is a first line of descending thirds from
measure 3 to measure 6. The ic3 A/C and ic4 C/A
dyads in measure lead to ic4 A# /F# in measure 5, followed in the next measure
by C/A
(as in measure 3), C#/A and E/C
(rh) (ic4, ic4, ic3/ ic3), culminating in the D/B dyad in the “half-cadence.”
The strikingly literal descent of ic4s prefigures other more or less obvious
scalar passages throughout the opus.
The first
four measures of II may almost be thought of as a re-composition of measure 1
of I. Note that the G/B dyad retains its registral position (rh), as does the
F# in measure 2 and the E
in measure 4 (spelled D# in measure 1). Only the D in measure 2 of II, is absent in
the opening measure of the first piece. Indeed, the pair of AUG0 and DIM0 are featured in both. In its terseness and concentration,
piece II offers the greatest number of symmetrical relationships since every event
is intervallically mapped onto every other.
Example 2: Schoenberg,
Sechs Kleine Klavierstücke, II
The third
piece contains the densest texture in the opus; yet it dwindles to a single
note - G - by measure 8. The dialectical process is a reductive one. A
thinning-out begins in measures 5 and 6, signaled by a converging symmetry in
the lower voices B
/C A/C# A/
D. Note that the group B
E
F A
begins and ends the piece (c.f. pitches marked 1-4 in measures 1 and 9).
Closure is further asserted by the reversal of the descending B
-E
octaves in the first measure in a mirror echo in the last measure. In addition, the group of four pitches in
measure two - B
C D
E
(numbered 5-8) - is partially retrograded in measures 3-4 (see pitches numbered
8, 6 and 5).
A long convergence of decreasing
interval size can be traced through the bass pitches in measures 1-3, (note
also the contrary voice leading in the rh in m.2) and is reflected further in
measure 4, before the convergence by contrary motion in measure 6 - B A A (descending) / C C# D
(ascending) – thus encompassing virtually the entire movement (see Example 3).
Example 3: Schoenberg, Sechs Kleine Klavierstücke, III
The planar structure of the opening of piece
III is an unusual combination of opposing textures and dynamics, suggestive of
polytonality. The symmetries in the first four measures are manifested in the
bass in octaves and its distinctive scalar motion together with its engagement
with the upper voices. The upper voices in these measures are rich in
symmetrical motions involving thirds and fourths. Especially important to the
melodic shape of the opening is the symmetry between measures 1 and 2 (+3 -3:
C# E/ A F#).
The
importance of contour symmetries in Opus 19 is often reinforced by subtle
echoes between movements. For example,
the B D# B in measure 5 is anticipated in II, m.4 (B E
B); the little contour symmetry E
E D# in measure 7 is a registral displacement of pitches that conclude piece I
(upper voice) and which re-emerge prominently in VI.
As in II,
important cadence points in III are determined by superimposed AUG and DIM cells. AUG0 and AUG2 form a half-cadence at measure 4, followed by DIM0 and DIM2 intertwined in measure 6
Densely
packed cells AUG0, DIM0, AUG2, DIM2 and AUG3 dominate III, nearly all of them
overlapping with the bass motion. AUG0
and DIM0 cells appear at the opening,
as they did in the previous two movements, and the AUG0 in measure 5 is a direct reference to the opening of both I
and II: the G/B dyad appears again, protrusively, in the same register as
measure 1 of I, and together with the D# revisits measure 4 of II. In III, m. 6, this continuity is reinforced
by the pairing of AUG0 and DIM2
- again, as in II, m. 6 - in
which pitches G, E D
and A
share registral identities with III, m. 6.
The premise
of this movement is the exposure and compression of a melodic line, supported
by occasional sharp chord-like punctuations.
The melody unfolds registrally in jagged skips through the opening, then
as smooth ascending lines in measures 4 to 6 and 7 to 9. A parallelism is maintained in the legato
responses to the angular opening in measures 2-3 and 7, where the C# E D#
figure is transposed to F# A G#.
The octave
displacement and temporal compression of measure 1 into the first beats of
measure 10 frames a similar relationship between measures 3-6 and 6-8. The
scalar D C F# G# A# B C (measures 3-6) - with all but F# and G# in a lower
octave – appears, also time-compressed in mm. 6-8. The initial D C in the
former group, after its fleeting grace-note reflection in m. 5, appears at the
end of the latter group, thus breaking up the whole-tone content of the pitch
collection.
IV is
primarily scalar, with references to scalar passages in other movements. The descending chromatic line in measures 2-5
(see Example 4) derives, as mentioned, from that of mm. 4-5 in the first piece
(see above). This derivation is reinforced by the appearance of the same AUG0 and AUG2 cells in measure 4, supporting a descending scale, just as
they do in I, m. 5. This is further
emphasized by the subtle reappearance of the 5/5 set (D) F G C in IV, m. 4,
which appears at the beginning of I and also comprises a major element of VI.
One of the most interesting structural details of
the piece is the shifting function of the A# B dyad that concludes the piece,
where it completes the linear F F# A# B symmetry and recalls the same tones in
identical registration within the unstable and interweaving melodic line
of mm. 7-8.
Example 4: Schoenberg,
Sechs Kleine Klavierstücke, IV
Opus
19, V
The fifth
piece - more or less a waltz - is based on accumulation of intervals. The
increasing density of the thirds - inner voices in measure 1 to pairs of thirds
in all voices at the end - suggest that the dialectical structure of the fifth
piece is in the transformation of single intervals into a texture composed of
these intervals, recalling the saturation of ic5s in the Kammersinfonie (i.e., transformation of quantity into quality).
The opening measure
is characteristic Schoenberg; the contrary motion between the hands encloses an
inversional relation between two diminished triads: C A G
(rh) and B D F (lh), offset by a sixteenth note. This is echoed in measure 2 in
a linear inversion between the left hand (G A
B)
and the right (A G# F#), the latter in augmentation and echoing the descending
contour of I, m.2 (B
A F# D#). The right-hand convergence in the opening two measures is paired with
another in contrary motion in the left hand (see Example 5) and in m. 4, IV
also recalls the polyphonic texture of I, m. 6 although with more structured
organization of trichordal retrogrades and inversions.
The fifth
piece is particularly referential. The AUG2
and DIM0 in the opening two measures
is a reinterpretation of the first three measures of IV: F C and B
are registrally invariant, and pitches D
B (bass clef) and A are reiterated. Also
note the quasi-tonal transposition of
the B
D
C A figure (IV, mm. 1-3) to G
B
A (V, opening) within a pseudo-F-major context.
Three
occurrences of AUG0 (measures 8, 9
and 12) are part of a network of references that spans all of I, II, III, IV
and VI. In particular, its occurrence in
measure 12 is in the same registration as that of the opening of the work (I,
m.1). The interesting superimposition of AUG1
and AUG2 at the conclusion, in which
one pitch in each is shifted to the other, recalls the conclusion of II and its
superimposed AUG0 and AUG3. Note the identical interval of separation
(ic1) for both pairs and the reversal in the lower left hand of the voice
leading of the exposed E-D
of m.11.
The contour symmetry in measures 7-8 recalls I, m.
3, in its shape if not in its pitch content, and the series of descending ic4s
in the left hand in measures 9-10 - as blatant as any of the internal
references in the work - clearly suggests the descending ic4s at the end of II.
The half-step motion of the contour symmetry also predicts the descending ic4
pairs in measures 9-10, which in turn anticipate the cadence. Pairs of thirds
also connect V and II:
II V
measure
5 measure 9
G
B/F# A# G B/F# A#
measure
6 measure 10
A C/A C# B D/A C#
(inversion)
measure
5 measure 12
G
B/F# A# G B/G B
measure
6 measure 14-15
A C/A C# rh A C/A C#
measure
7 measure 14-15
F
A lh F A/E
G#
Figure 6:
Schoenberg Comparison of Third Pairings in Op. 19, II and V
Example 5: Schoenberg,
Sechs Kleine Klavierstücke, V
Op.
19, VI
A tolling figure runs through the brief final
movement, which Schoenberg composed after hearing of Mahler’s death. It owes its retrospective and pensive
character not only to the sound quality of the tolling intervals, but also
because of strands of reference to previous movements. In fact, there is very
little in the movement that cannot be found in earlier ones.
Tones B and A in the upper half of
the tolling figure are the initial notes of the entire piece; the F# occurs at
the end of measure 1. (Note that the three pitches appear an octave higher in
VI, but in the same 6/9 registral relation to each other.) The other element of
the tolling figure - F C G - appears in I, m, 1 as well, and in the same
register. In VI the DIM0 in measures
4-5 linking the two halves supports an important long-range connection between
the first and last movements.
The DIM0 in measures 4-5 is accompanied - unusually - by a D# in
octaves. The upper note is part of the
contour symmetry D# E D#, which first occurs in the last measure of I (upper
voice, with adjacent D# octave). This detail is also one of the most telling
and poignant recollections in the set of pieces (also see III, m. 7: E E E, as well as in the
inner-voice E-E-E in m. 9 at the close
of this piece).
The final movement also affirms the
quartal process and connects it with the opening of the work. The second half
of the tolling figure - F G C - is transposed to B F C
in measure 6, and shares two pitches with the F C G cell. In fact, the same
quartal hexachords can be found in both movements:
VI 6 m. 6
D
G C F B (D# in
previous measure)
I,
m. 2
D
G C F B (rh) (D#
in previous measure)
Figure 7:
Schoenberg, Comparison of ic5
Collections in Op. 19, I and VI
This
emergence is based on the accumulation of a number of details throughout the
work (excepting the third-obsessed piece II).
-
The left hand pitches in III, mm. 1-2 can be expressed
as a fourth cycle (A E B F C),
which shares three pitches with the quartal material in VI, (B F C);
another quartal figure follows in measure 3 (A D G A C).
-
The F C G D subset appears in IV, m. 4 in the
left hand, and also in mm. 11-12.
-
A nearly complete quartal hexachord con be
found in V, m. 8: A# C/G F/D, where the G C and F are in their original
register in I.
The chart in Figure 8 traces the
emergence of perfect-fourth intervals with triangular note heads indicating
those in their original registral positions in. I.
Measure 9 contains the pitches C F#
G G# E E, all of
which (except for C# and D) appear in I, measure 1. Note that the measure 9
pairing of AUG0 and AUG1 also references I, m. 1. The pair
of symmetries 5/5 and 10/10 at measures 6-7 point toward the final measure -
and the end of the work - which closes with a symmetrical 14/14 (B-A / BA) echo wie ein Hauch: “like a breath.”
Figure 8: IC5
Collections in Op. 19
Example 6: Schoenberg, Sechs Kleine Klavierstücke, VI