Two New Digital Techniques For The Transfiguration Of Speech Into Musical Sounds

Two New Digital Techniques For The Transfiguration Of Speech Into Musical Sounds¹

Richard Boulanger

Abstract

Speech and music have been inextricably entwined from their very beginnings. In the Western musical tradition there have been such manifestations as chant, recitative, Sprechstimme, and text-sound. Each of these can be seen as a translation of a limited portion of the total speech into the musical vocabulary of the age - speech intonation into melodic formulae, prosodic rhythm into restricted patterns and sequences. Two digital filtering techniques provide new means for transforming, speech into music. Mathematically these techniques can be described as linear filtering operations. Musically they can be understood as means of specifying and controlling resonances. The first, the Karplus-Strong plucked-string algorithm, loosely models the acoustic behavior of a plucked string. The second, fast-convolution, is a procedure for obtaining the product of the two spectra. The contribution of this research lies both in the novel musical interpretation of these techniques and in the elucidation of their musical use. A wide variety of musical applications are demonstrated through taped sound examples. These include specifiable echo and reverberation, generalized cross-synthesis, and dynamically controllable and tunable string resonance, all utilizing natural speech. Some of these resemble prior musical applications of speech while others represent entirely new possibilities.

A large body of research has addressed the application of digital signal processing techniques to the problems and technical concerns of speech communication², concerns ranging from the digital transmission and storage of speech, to its recognition, enhancement, and synthesis. Applications have included telecommunication, automated information services, reading and writing machines, voice communication with computers, and voice-activated security systems, to name a few.³ Speech has been a continuing issue in music as well. From the time of the Greeks to the present, innovative compositional applications of speech have defined and redefined the boundaries of the field. Concerns have included the intelligibility of the sung/spoken word and the control of its pitch, onset, duration, amplitude, and timbre. Applications have included recitative, Sprechstirnrne, chant, and opera, to name a few³. Each of these innovative compositional applications can be seen in part as a response to technological advances, both advances introducing new tools and advances offering new insights into the behavior and utility of existing tools. The most. recent and potentially most powerful conceptual and practical tools which have become available to the composer are those of digital signal processing. While the compositional utility of signal processing techniques is but a peripheral concern to the speech processing community, techniques such as the phase vocoder and linear predictive coding offer the composer tools to readdress fundamental concerns regarding speech as music. In this paper, I demonstrate the musical utility of two recent digital techniques, the Karplus-Strong plucked-string algorithm, and fast convolution, and show how they can be used to transfigure can normal speech into musical sound, creating effects which are both new and powerful.

Of Speech and Music

The precise beginnings of music are unknown, though several theories place its origins in either exaggerated speech or in the ecstatic, percussive, dance-oriented expression of biological and/or work rhythms.⁴ An interesting alternative is proposed by Leonard Bernstein in The Unanswered Question: Six Talks at Harvard.⁵ He suggests that song is the root of speech communication and not the other way around. In support of this claim he cites the fact that vocalizations of non-human primates consist almost entirely of changes in pitch and duration, and that speech articulations appear to be characteristically human. According to Pribram, such observations suggest that "at the phonological level speech and music begin in phylogeny and ontogeny with a common expressive mode."⁶

Whether or not music and speech evolved from a common expressive mode, it is generally considered that speech is a special kind of auditory stimulus, and that speech stimuli are perceived and processed in a different way from nonspeech stimuli. In support of this view Brian C.J. Moore points to evidence derived from studies in categorical perception, which indicate that speech sounds can be discriminated only when they are identified as being linguistically different; from studies of cerebral asymmetry, which indicate that certain parts of the brain are specialized for dealing with speech; and from the speechnonspeech dichotomy, in which speechlike sounds are either perceived as speech or as something completely nonlinguistic.⁷

A number of innovative historical manifestations of speech as music exist. These are traceable as far back as the Greeks. The issue is not whether the solutions to the problems associated with speech as music resulted from intuitively tapping the common root of the two modalities (speech and music), or whether they merely exploited the speech/non-speech dichotomy and thereby demonstrate that speech sounds, when presented in non-linguistic constructions, are automatically transformed into speech-music (i.e., non-speech). Those are issues for musicological and psychological study and debate.

Valid historical solutions do exist, and they can often be equated with musical innovation. As such these innovative uses of sound continue to redefine the limits of musical possibility. The following historical review highlights two innovative musical solutions, solutions which resulted from the application of new technology to the fundamental problems of speech and music. Granted, the history of music will provide the final say - the ultimate validation of all theoretical propositions, still there is no denying that speech is transfigured into musical sound in pieces such as Reich's Come Out, Eno's My Life in the Bush of Ghosts, Berio's Thema (Omaggio a Joyce), Reynolds' Voicespace, and Lansky's Six Fantasies on a Poem by Thomas Campion.

Two Current Digital Techniques

Until recently, the technology did not exist by which the acoustical components of speech could be extracted for the purpose of systematic compositional exploration. Now that it does, the potential for musical advancement rests on the innovative applications of it.

Linear Predictive Coding and Its Musical Use in Dodge's Speechsongs

Charles Dodge is most notable for his pioneering work in the musical applications of computer speech synthesis. Using the computer and an analysis-based subtractive synthecic technique known as linear-predictive coding (LPC) Dodge composes a music of true Speech melodies - speechsongs. With LPC, any word or phrase which has been analyzed can be resynthesized directly. However, the true musical utility of LPC lies in the fact that the analysis operation effectively ^-decouples^- the parameters of pitch, time, and spectrum. Thus the composer can arbitrarily and independently control these three fundamental components of the analyzed speech in the same way that he would traditionally Compose and orchestrate the notes and rhythms of a traditional piece of instrumental or vocal music.

For the first time we have in electronic music the possibility of making something extremely concrete - that is, English communication of words - which can be extended directly into abstract electronic sound. In the past, there's been quite an abutment between the two. On the one hand, you've had music such such as Milton Babbitt's, with its sophisticated differentiations of timbre, pitch, and time; and on the other hand, you've had musique concrete, consisting of the reprocessings of sounds made with microphones. The synthetic speech process combines the two in quite an interesting way. It bridges that gap between recorded sound and synthesized sound.⁸

Linear predictive coding is a method of designing a filter to best approximate the spectrum of a given signal. Although the approximation gives as a result a filter valid over a limited time, it is often used to approximate time-variant waveforms by computing a filter at certain intervals in time. This gives a series of filters, each one of which best approximates the signal in its neighborhood.⁹ In his survey paper on the signal processing aspects of computer music, James A. Moorer describes the steps involved in the Dodge "speechsong^- analysis to synthesis process. It begins with reciting the voice material into a microphone which is connected to an analog-to-digital converter on the computer. The speech is then analyzed and the analysis produces as intermediate data the voicing information (whether a periodic or noise excitation is to be used), the pitch of the speech (if it is voiced), and the filter coefficients, all at regularly spaced points in time. This data can be used to resynthesize the original utterance directly, or it can be modified. For example, the utterance can be re-synthesized at different rates by changing the parameters (pitch, filter coefficients, voiced/unvoiced decision) faster or slower than they occur in the original utterance. Or the pitch can be changed without changing the temporal succession simply by multiplying all the pitches by a fixed scale factor.¹⁰ Normally if one takes recorded speech and merely speeds up or slows down the waveform itself, the fundamental frequency of the speech is changed as well as the tone quality. However, by first analyzing the speech, one can change the timing or the fundamental of the speech independently.

It is also possible, using the LPC analysis/synthesis technique, to modify speech in ways which would be impossible for a real speaker to do. Typically, white noise is used as the source function for the resynthesis of aperiodic speech sounds and a wide-band periodic signal such as a pulse train is used as the source function for the resynthesis of the voiced portions of speech. However, other driving functions might be employed. For example one might substitute a more complex signal such as the recording of an orchestra for the pulse train and thereby achieve "talking orchestra" effects. Dodge often mixes varying degrees of noise in with the pulse train to create a sung/whispered speech (i.e., Sprechstimme).

Both the "talking orchestra'^. and Dodge's synthetic Sprechstirnme effects are examples of what is called "cross-synthesis." One often refers to cross-synthesis to characterize the production of a sound that compounds certain aspects of sound A and other aspects of sound B.¹¹Thus, since the physical model of speech which is manifest in the LPC technique separates speech into two, fairly independent components, the quasi-periodic excitation of the vocal cords and the vocal-tract response (i.e., • formant structure) which is varied through articulation, the possibility of independently controlling either of these components of speech^- by "certain aspects" of other sounds only requires substitution. The results of these changes are potentially musically significant.

The Phase Vocoder - Moorer's Lions are Growing

Lions are Growing (1978) is a "study" by Andy Moorer which uses computer treatment of the sounds of the human voice. The clarity, range, and fidelity of the synthetic speech in it represent a significant advance over that in Dodge's speechsong work. Actually, the analysis-synthesis technique used to create Lions are Growing is not LPC. Rather it uses the phase vocoder which, particularly because of its potentially very high-fidelity output, has a far greater musical potential. Of the piece Moorer writes:

This study uses as text a poem by Richard Brautigan entitled "Lions are Growing." All the sounds are based on two readings of the poem by Charles Shere. These two readings were fed into the computer, then decomposed and analyzed by the computer into pitch, format structure, and other parameters. The composition of the piece, then, consisted of resynthesizing the utterances, applying various transformations to the pitch, timing, and sometimes formant structures. The resulting transformed sounds were mixed together to form thick textures with as many as 30 voices sounding simultaneously. Computer-generated artificial reverberation was then applied and the sounds were distributed between the two speakers. All but a very few of the sounds in this study then are entirely computer synthetic, based on original human utterances.

In the phase vocoder, an input signal is modeled as a sum of sine waves and the parameters to be determined by analysis are the time-varying amplitudes and frequencies of each sine wave. Since these sine waves are not required to be harmonically related, this model is appropriate for a wide variety of musical signals. By itself, the phase vocoder can perform very high-fidelity time-scale modification or pitch transposition of a wide range of sounds. In conjunction with a standard software synthesis program, the phase vocoder can provide the composer with arbitrary control of individual harmonics.¹²

Historically, the phase vocoder comes from a long line of voice coding techniques which were developed primarily for reducing the bandwidth needed for satisfactory transmission of speech over phone lines. The term vocoder is merely a contraction of the words "voice coder... Of the wide variety of voice coding techniques the phase vocoder, so named because it preserves the time varying "phase" of the input signal as well as its frequency and magnitude information, was first described in a 1966 article by Flanagan and widen. However, only in the past ten years, primarily due to improvements in the speed and efficiency of implementations of the technique, has the phase vocoder become so popular and well understood, at least in signal processing circles.¹³

Although undeniably a beautiful piece, Moorer's Lions are Growing does not represent the "next" innovative computer-based solution to the problem of speech as music. Viewed from the historical perspective, it is clearly a conventionalization of the Dodge innovation. As such, it merely demonstrates, in a charming and humorous fashion, the degree to which this new analysis-synthesis technique (the phase vocoder) can improve speechsong" fidelity. Obviously high-fidelity is an important factor in music, but it is not necessarily a significant or innovative one.

An innovative speech-music application of the phase vocoder has recently drawn the attention of composers and researchers at the Computer Audio Research Laboratory at the University of California in San Diego. It results from the time-expansion of speech by extremely large factors (i.e., between 20 and 200). In these cases, the speech is no longer discernible as such, but rather, the underlying structure of the sound is brought to the perceptual surface. This process of extreme time-expansion "magnifies," in a sense, the ^-microevolution^- of the spectral components of speech, and effectively transforms spoken text into musical texture. This application employs the phase vocoder as a "sonic microscope" to reveal the "symphony" underlying even the shortest of utterances. A music based on that which is revealed by these exploded views could prove quite significant and the phase vocoder represents a powerful new tool for music whose significance has yet to be fully recognized or musically demonstrated.

Two New Digital Techniques

The Karplus-Strong Plucked-String Algorithm as a Tunable Resonator

Techniques for the computer control of pitch have an obvious significance for music. In particular, linear prediction and phase vocoding were cited as two recent computer-based methods for infusing speech with an arbitrarily specifiable pitch. But these techniques demand both considerable computational resources and considerable mathematical sophistication on the part of the program. In this chapter an attractive new alternative to these techniques is presented.

The basis for this technique is the Karplus-Strong plucked-string algorithm.¹⁴ The algorithm itself consists of a recirculating delay line which represents the string, a noise burst which represents the "pluck," and a low-pass filter which simulates damping in the system_ Applications of this algorithm to date have focused primarily on extending its ability to imitate subtle acoustic features and performance techniques associated with real strings and string instruments. In contrast, this chapter investigates the musical utility of the system as a tunable resonator.

The Ideal String

Any dynamic system has two types of response - a forced response, and a natural response. The natural response is that which continues after all excitation is removed. In the case of a violin string, the natural response is that which follows the pluck. The forced response, on the other hand, is that which occurs in the presence of some form of excitation. In the case of the violin string, forced response occurs when the string is bowed. The overall response of the system is equal to the sum of the forced response and the natural response.

An ideal string¹⁵ is a closed physical system consisting of an infinitely flexible wire, fixed at both ends, by anchors of infinite mass, and characterized by three independent variables: mass, tension, and length. When its vibration is excited by a one-time supply of energy, such as a pluck, two wave pulses propagate to the left and right of the point of excitation, reach the anchors (which act as nodes), and reflect back in reverse phase. A short time after the input has ceased, a series of "standing waves" results. The specific point of excitation determines which standing waves are present.

Standing waves or "modes of vibration" represent the only possible stable forms of vibration in a system. In the case of the ideal string, only those standing waves which "fit" an integral number of times between the anchor points are possible, because destructive interference would effectively cancel out all others. Standing waves thus have frequencies that are integral multiples of a fundamental frequency determined by the string's mass, tension, and length. For both the ideal and the real string, altering any of these three parameters alters the fundamental frequency.

An important distinction between ideal and real strings concerns the dissipation of energy. In the ideal string, those vibrational modes which have not been canceled out will vibrate indefinitely. But in a real string, all the wave energy gradually dissipates via internal friction (because a real string is not infinitely flexible and infinitely thin) and through the anchors (which, in the case of a real string, are not of infinite mass).

Another notable distinction concerns the property of stiffness in real strings. Due to stiffness, the frequencies of higher vibrational modes of real strings are not exact integer multiples of the frequency of the fundamental mode. Therefore stiffness can significantly affect the timbre of real strings.

The Karplus-Strong Plucked-String Algorithm

The Karplus-Strong plucked-string algorithm is a computational model of a vibrating string based on physical resonating. In 1978 Alex Strong discovered a highly efficient means of generating timbres similar to "slowly decaying plucked strings" by averaging successive samples in a pre-loaded wave table. Behind Karplus and Strong's research was the effort to develop an algorithm which would produce "rich and natural" sounding timbres, yet which would be inexpensively implementable in both hardware and software on a personal computer. Since their algorithm merely adds and shifts samples, it meets the above criteria. But the limitations of small computer systems, particularly the absence of high-speed multiplication, impose serious constraints on the algorithm's general musical utility. Still, the Karplus-Strong plucked-string algorithm does allow for a limited parametric control of pitch, amplitude, and decay-time.

Frequency resolution depends largely on the length of the wave table and the sampling-rate. A small wave table results in wide spaces between the available frequencies. A larger one, while offering better frequency resolution, can "adversely" affect the decay times. In either case. since the length of the wave table must be an integer, not all frequencies are available.

According to the natural behavior of the system, the output amplitude is directly related to the amplitude of the noise burst. As a means of controlling the output level Karplus and Strong recommend loading the wave table with different functions or employing other schemes for random generation. They further suggest that the pluck itself might be eliminated by simultaneously starting two out of phase copies and letting them drift apart.

Like frequency, the decay-time resolution is dependent on the table-length. Higher pitches will naturally have shorter decay-times than lower pitches. This is due to • the fact that higher frequencies are more attenuated by a two-point average, and that a higher pitch means more trips through the attenuating loop in a given time period. To stretch the decay-time of higher pitches, Karplus and Strong suggest filling the wave table with more copies of the input function; to shorten the decay-time of lower pitches, they suggest using alternate averaging schemes (such as a 1-2-1 recurrence).

The Jaffe-Smith Extensions

An implementation of the plucked-string algorithm on a high-powered computer by Jaffe and Smith allows several modifications and extensions which substantially increase its musical utility.¹⁶ In particular, Jaffe and Smith address the problems associated with the arbitrary specification of frequency, amplitude and duration. They consider the Karplus-Strong plucked-string algorithm to be an instrument-simulation algorithm which efficiently implements certain kinds of filters, and they point out that, from the perspective of digital filter theory, the system can be viewed as a delay line with no inputs.

To compensate for the difference between the table-length-based frequency and the desired frequency, Jaffe and Smith suggest the insertion of a first-order all-pass filter. Since an all-pass has a constant amplitude response, it can contribute the necessary small delays to the feedback loop without altering the the loop gain (i.e., the phase delay can be selected so as to tune to the desired frequency and thereby adjust the pitch without altering the timbre).

As a means of controlling the output level, Jaffe and Smith recommend that a one-pole low-pass filter be applied to the "pluck." This alters the spectral bandwidth of the noise; with less high frequency energy in the table, the audible effect is of the string being plucked lightly. Another possible means is to simply turn the output on late, after some of the high frequency energy has died away.

To lengthen the decay-time of higher pitches, Jaffe and Smith recommend weighting the two-point average. To shorten the decay of lower pitches, they suggest adding a dampening factor. Since the damping factor affects all harmonics equally, the relative decay rates remain unchanged.

As well as their solutions to some of the algorithm's fundamental limitations, Jaffe and Smith recommend the inclusion of several other filters as a means to simulate subtle acoustic and performance features of real plucked strings. For example, they suggest that a comb filter can be used to effectively simulate the point of excitation by imposing periodic nulls on the spectrum. Another filter can be incorporated to simulate the difference between "up" and "down" picking. They also note that an allpass filter can be used to stretch the frequencies of the upper harmonics out of exact integer multiples with the fundamental and thereby effectively simulate varying degrees of string stiffness.

In the cmusic software synthesis language the fltdelay unit generator is an implementation by Mark Dolson of the Jaffe-Smith extensions with several additions. Most significant among these is that he allows an arbitrary input signal to be substituted for the initial noise input - an extension originally suggested by Karplus and Strong, but not otherwise pursued. This feature expands the scope of the model from one which simulates a limited class of plucked-string timbres to a general-purpose tunable resonance system.

A Conventional Application: The Plucked-String

Sound Example III.1A¹⁷ demonstrates the general musical utility of the jitdell unit generator in its typical application - as a means of producing plucked-string timbres. The main feature of this example is that it clearly reveals a • "natural-sounding" timbre which is indeed "string-like" and remains so throughout a wide range of pitches and under a wide variety of "performance situations." Furthermore, although the sound is clearly string-like, it does not particularly sound like any identifiable string or stringed instrument.

The first and second sections display a change in timbre associated with pitch height. As with real stringed instruments, higher tones sound more brittle than lower ones. Section three demonstrates the added richness which results from multiple "unison" strings as found, for example, in the design of most conventional keyboard instruments. The fourth section demonstrates fltdelay's ability to simulate a variety of string types, (e.g., nylon, metal, metal-wound). These different "strings" result from the various parameter settings of place and stif^f. Parametric control of string stiffness is one example of the unique features of this computer model which have no real world parallel. The fifth section demonstrates a technique which is possible on some stringed instruments but not on all - glissando. Without the physical limitations of real strings, glissandi of any contour, range, and speed are now possible.

By the very nature of this example, the musical utility of the algorithm is revealed, and its ability to serve in numerous conventional applications is obvious. A more comprehensive musical display of the Karplus-Strong plucked-string algorithm's extensive and diverse sound repertoire can be found in David Jaffe's four-channel tape composition Silicon Valley Breakdown.¹⁸

When writing for tape and live instruments, electro-acoustic composers have often contrasted, complimented, and/or challenged live performers with synthetic shadows or counterparts of their acoustic instruments. In these situations the tape often plays the part of the acoustic instrument's alter-ego. David Jaffe's May All Your Children Be Acrobats (1981) is such an example. In the composition a computer-generated tape (which features Karplus-Strong plucked-string generated sounds) accompanies a female voice and eight real plucked-sting instruments (guitars). This piece, and others which have followed, demonstrate that in its conventional use, the Karplus-Strong plucked-string algorithm provides a new, versatile, and flexible tool for the continuation of this frequent musical practice.

A New Application: The String-Resonator

The utility of the Karplus-Strong algorithm in producing a wide variety of natural sounding plucked-string timbres has been established. What is far less appreciated, though, is that the Karplus-Strong plucked-string algorithm can also be used as a resonator.

The basic property of any resonator is that it can only enhance energy which is already present in the input at the resonant frequencies. As a consequence, the sound of any resonated source can be thought of conceptually as the dynamic spectral intersection of the source and resonator. Mathematically, the spectrum of the resonated source is the product of the two spectra. This product is a spectral intersection in the sense that it is nonzero only at frequencies at which both the input and resonator spectra are non-zero. The intersection is dynamic in that the spectrum of the source is dynamically changing in time.

This concept is particularly relevant for a speech input because speech consists of both "voiced" and "un-voiced" segments, and because the voiced segments typically have a constantly varying pitch. This means that the pitch of the voiced segments will not usually match the pitch of the resonator, and the spectral intersection will be null. However, the unvoiced speech will always have energy in common with the resonator, regardless of the resonator's pitch. Thus, it is actually the unvoiced segments of speech that are infused with pitch. Furthermore, what is actually being said becomes quite important. For instance, a resonator will have little effect if its input is simply a sequence of vowels.

This is in contrast to the techniques of Chapter II (linear prediction and phase vocoder) in which the pitch of the voiced segments is controlled. In the case of linear prediction, pitch control is achieved by setting an excitation signal to the desired pitch; in the case of the phase vocoder, the voiced pitch is simply transposed.

When using the Karplus-Strong plucked-string algorithm as a resonator of speech, the resulting percept is very much like the sound of someone shouting into a piano with a single key depressed. The primary character of the model (i.e., its string-like timbre) is also the most salient characteristic of any speech which is resonated with it. This percept is so strong that it no longer makes sense to think of the model as a plucked-string or as jltdelay. Rather, by virtue of this unique application and the general timbral character of the resulting sound, the algorithm can be more appropriately understood as a tunable "string-resonator."

An important distinction between using a real string as a resonator and the Karplus-Strong string-resonator has to do with coupling. In the case of the string-resonator the coupling is much better than in real life; thus, far more of the voice energy is delivered to the string.

For musical applications, another important consideration is the relation between the pitch of the voice and the pitch of the resonator. When the two are close in pitch, they tend to present a more fused percept. As the pitches become more disparate, there is still a clear sense of pitch, but the resulting sound is divided into two components with the resonated pitch above and the speech below. This is illustrated in Sound Example III.2A which demonstrates the behavior of the string-resonator over a four octave frequency range.

The example has been divided into three sections based on the degree of fusion between spoken text and resonator. In the first section, the voice and the string-resonator are heard as a relatively fused percept. The apparent pitch is that to which the string-resonator is tuned. In the second section, as the pitches rise, the two components - voice and tuned resonance, become progressively more distinct, and become parallel streams by Fs(4). A feature of the third section is the bright ringing "sparkle" associated with the noise components of the spoken text.

By virtue of the string-resonator's ability to effectively infuse natural speech with pitch, a number of new musical applications become possible. Sound Example III.2B demonstrates one such musical application which I call string-chanting. The instrument is similar to the one above but for two additions: parametric control of amplitude and parametric control of string stiffness. These two additional controls allow for individual, and variable setting of the balance and timbre of each string-resonated voice.

The score divides into two sections. In the first, four voices enter independently, pseudo-canonically, one approximately every 1.5 seconds. In the second section, six voices enter simultaneously and cut off together at the end of the single line of text which is the input.

A String-Resonator with Varying Stiffness

The Jaffe and Smith extensions of the Karplus-Strong plucked-string algorithm also extend its utility as a string-resonator. In particular, their addition of an all-pass filter to simulate string stiffness provides control of the resulting timbre of the string-resonated input and thereby increases its general utility.

To this point, the character of string-resonated speech has been a predominantly metallic timbre which has been completely harmonic. This naturally leads to comparisons with the contemporary musical practice of shouting into an open piano with various keys depressed (e.g., Crumb's Makrokosrnos). Without the Jaffe and Smith addition to simulate the various degrees of stiffness associated with real strings, this metallic timbre would always dominate the character of any string-resonated input. However, by simply increasing the string-resonator's stiffness (i.e., stretching the partials), the character of Sound Example III.3A is transformed from a dark metallic timbre to a delicate "glasslike" one.

Control of timbre musically significant, and various settings of stiff correspond to different string-resonated timbres. That the string-resonator's stiffness can be altered parametrically further increases its utility, by allowing the note-level control of subtle variations in spectral shading. Thus, stiff can be seen as the string-resonator's general tone control.

A String-Resonator with Varying Pitch

With the addition of a single unit generator to the basic string-resonator instrument it is possible to alter the frequency of the string as a function of time. This musically useful extension is made possible by the design of the cmusic fltdelay unit generator.

One of the basic design features of fitdelay is that its pitch argument accepts values via an input/output (i/o) block. An i/o block is like a patchcord. It holds the output of one unit generator in order to allow its use as the input of another unit generator. In this case, the output for the dynamic control of the string-resonator's pitch can come from cmusic's trans unit generator.

The trans unit generator allows for the parametric specification of the time, value, and exponential transition shape of a function consisting of an arbitrary number of transitions. In Sound Example III.4 a three point exponential transition is specified. The timing of the function is fixed for all notes (i.e., 0, 1/3, 1) and the three frequency values of the pitch shift are specifiable parametrically.

Sound Example III.4 divides into two sections. The first consists of six notes, each with a unique pitch transition (i.e., up and down, up and up, etc.) and each featuring a different range and limit. None of the notes overlap.

The second section is a musical application of pitch shifting "string-resonators." All of the notes presented in the first section are reused, and several additional notes are added. The duration of all notes is doubled and many of them overlap.

It is interesting to observe the degree of fusion under extreme pitch shifts such as these. In a number of cases, the words themselves sound as if they have been stretched out of proportion. The mutation of the spoken word "world" is an example of the type of sounds which result from a recirculating delay whose pitch (i.e., delay) is continuously shifted.

As regards the implementation of the model, a relevant point is that the decay factor is set at the beginning of a note. This corresponds to setting the appropriate damping in the system whereby a note will turn off at the end of the duration set in p4. When the pitch changes during the course of the note, the decay factor will remain constant. Normally a low tone would require a great deal of attenuation for it to have the same effective damping as a higher tone. Thus, since the effective damping is not kept constant when pitches are shifted from high to low, there is a noticeable shift in perceived sound quality, a ^-boominess^- at the bottom end of a downward gliss.

The ability to vary the pitch of the string-resonator during the course of the note is another extension of its musical utility. Given dynamic pitch control, one can easily infuse the speech with not only pitch, but with musical vibrato, portamento, or glissando.

Within the past ten years, a growing number of singers and composers have experimented with the production and compositional specification of a wide range of extended forms of vocal production.¹⁹ Example is a string-resonator emulation of some of these musical practices (e.g., Roger Reynolds' Voicespace, Deborah Kavasch's The Owl and the Pussycat, and Arnold Schoenberg's Pierrot Lunaire). In this regard, this sound example demonstrates a feature of the string model which has no real-world parallels. It is not possible to simultaneously vary the tuning of an arbitrary number of resonators over such an wide pitch range and with such accuracy except, perhaps, by demanding such from the vocal-tract resonant systems of a chorus of extended-vocal-technique specialists such as Diamanda Galas, or Philip Larson.²⁰ Some of the extreme frequency shifts in this specific musical example are not humanly possible.

String-Resonators as Echo-Reverberators

The musical utility of the string-resonator is not limited by the human capacity for pitch discrimination (ca., 20Hz to 20kHz). In particular, when the resonator is tuned to frequencies below 10Hz the mechanism of the model is revealed; repetitions of the input are readily perceived as it recirculates through the delay-line (i.e., "the string"). This extension of the string-resonator can be more appropriately thought of as a "string-echo."

The frequencies of the four notes in Sound Example III.5A range from 4Hz to 19Hz in 5Hz steps. When tuning the resonator to such low frequencies the maximum length of the delay-line must be altered from its default length of 1K-samples to 16K. This is because the lowest fundamental frequency which can be generated by fltdelay is directly related to the length of the delay-line by the equation:

F₀ = R / L

where F_a is the fundamental frequency, R is the sampling rate, and L is the length of the delay-line in samples. Thus with a 16K-sample maximum delay and a 16KHz sample-rate, fltdelay can accurately produce signals with fundamental frequencies as low as 1Hz.

The sound of the first note, at 4Hz, is an echo of the input at a rate of 4 times per second. The second note, at 9Hz, still has some sense of repetition associated with it, but it also sounds as if someone is speaking into a large metal cylinder. This is remarkable for a frequency so low. The third note, at 14Hz, presents more of a flutter than an echo, and the fourth, at 19Hz, is pitched, but with a strong sense of roughness.

A point to note is that string-echo via fltdelay is different from echo produced via a recirculating comb filter. Fltdelay has a frequency dependent loop gain whereas the recirculating comb filter does not. It is precisely this frequency dependent loop gain which accounts for the characteristic coloration of the model (i.e., its stringlike timbre). This is because, in fltdelay, as is the case in a real string, high frequencies are more rapidly attenuated than low frequencies.

The technique of echo has long been a staple of electro-acoustic composers, initially in the form of complex tape loop mechanisms (e.g., Oliveros' I of IV), later via analog delay circuits, and presently through the proliferation of portable, programmable digital delay units. However, a significant feature of string-echo not shared by any of the aforementioned devices is that of dynamic repetition-rate control (i.e., pitch control) such as was shown in Sound Example I11.4A.

In addition to the echo and flutter effects which predominate at repetition rates below 20Hz, there is also another class of effects at the low end of the audible pitch range. Sound Example III.5B, which illustrates these, divides into two sections. The first is a sequential entry of four rising pitches, and the second, a succession of two chords. This sound example parallels the 111.2 series which also featured a rising series of string-resonated pitches followed by a multi-voice chord. The only significant difference between the two examples is that III.5B spans a lower pitch range (C₀ to C₂). The sound results of the two examples, however, are not parallel. In particular, when string-resonated chords are played in this low register, they are not perceived as discrete harmonies at all. Rather, they give the impression of a highly colored reverberance, a reverberance which is literable tunable.

A strong sense of pitch dominates each of the four notes in the first section of Sound Example III.5B. Although the degree of fusion is clearly different for each note, and gets stronger as the pitch of the string-resonator gets higher, this does not detract from the general perception of tuned resonance. In the second section, however, when several differently tuned string-resonators play simultaneously, the predominant sense is of a complex and diffused reverberance.

Perceptually, this is not the effect that one might have expected, particularly given that string-resonated chords are easily perceived as such when the component frequencies are just one or two octaves higher, and, that even in this register, single string-resonated notes are so clearly pitched. Low-register string-resonated chords begin to approach a realistic reverberant situation in which many different delay times are superposed.

Previously, all changes in the settings of the instrument were made at the start-time of the note and were determined by the settings of the various parameters. Now, with a global design, changes can affect an instrument during a note rather than only at its outset. This effectively models the cmusic orchestra on a real orchestra in which instrumentalists perform their own parts, responding to all its commands for execution, (i.e., phrase, dynamic, and timbre indications), while simultaneously responding to the general directions of the conductor.

The score for example III.6C is in stereo. One channel contains the utput of "voice," the other contains the output of the "sympathetic." The pitch of the source resonator remains constant (87 Hz), while the sympathetically-resonated voices alternate from a non-equal-tempered triad to an equal-tempered one.

Sound Example III.6D demonstrates yet another global score model using sympathetic excitation. The score format has been simplified, by assimilating the former's output instrument into the sympathetic resonator instrument.

Whereas in the previous example, all three sympathetically-resonated voices had the same setting, in this one their finals and respective timbres are slightly different.

In both musical examples sympathetically-resonated voices significantly enrich the sonic character of the basic string-resonator. Musical parallels for resonant techniques such as those demonstrated in examples III.6C and D are also found in the contemporary literature. For example, in Berio's Sequenza X for solo trumpet (1985), the trumpeter plays into an opened piano while an onstage pianist silently depresses certain notes and chords which effectively underscore the solo part with the desired harmonic resonances. However, unlike those musical examples which employ pianos as resonators, this particular extension of the string-resonator allows for a continuous pitch shift of an infinite number of sympathetically-resonated voices. The general musical utility of the string-resonator is substantially increased by an ability to alter and control its mode and degree of excitation.

Generalized Resonators via Fast Convolution of Soundfiles

It was shown that the Karplus-Strong plucked-string algorithm provides the basis for a simple yet powerful new technique for infusing speech with musical pitch. The perceptual effect is akin to that of speaking into the piano. But now, suppose that we wish to speak into some other instrument. How can this new effect be obtained?

The acoustical difference between the concert hall and the shower stall is that each is the manifestation of a slightly different filter. The pinnae of the ear, the cavity of the mouth, the body of a violin, the wire connecting speaker to amp, any medium through which a musical signal passes can be considered a filter. And via the computer, it is possible to mathematically simulate any filter, given the proper description.

One means of implementing a filter is via direct convolution. Convolution is a point-by-point mathematical operation in which one function is effectively smeared by another. When an arbitrary signal is convolved with the impulse response of a filter, the result is the filtered output.

Traditionally, convolution has been employed primarily to efficiently implement certain types of FIR filters. Thus, the required impulse response has typically been obtained as the result of a standard filter-design algorithm. In principle, however, any digital signal can serve as the impulse response in the convolution process. It is precisely this observation which constitutes the starting point for the chapter to follow. Digital Filters

Linear filtering is the operation of convolving a signal with a filter impulse response.²⁴ Signals are represented in two fundamental domains, the time-domain and the frequency domain. Addition in one domain corresponds to addition in the other domain. Thus, when two waveforms are added, it is the same as adding their spectra. Multiplication in one domain corresponds to convolution in the other domain. Thus, when two waveforms are multiplied, it is the same as convolving their spectra. Similarly, when two spectra are multiplied, their waveforms are convolved. Thus, since linear filtering is the operation of convolving a signal x(n) with a filter impulse response h(n), it is equivalent to multiplication in the spectral domain.

Convolution, like addition, multiplication, subtraction, or division, is a point-by point operation which can be performed on two digital waveforms. It is the process by which successively delayed copies of x(n) are weighted by successive values of h(n) and added together, effectively "smearing" x(n) with h(n).

Thus, if h(n) = u(n) (i.e., the function of x(n) is convolved with a single impulse), it is clear that x(n) remains unchanged. The impulse is said to be an " identity" function with regard to convolution because convolving any function with an impulse leaves that function unchanged. If the impulse is scaled by a constant, the result is x(n) scaled by the same constant. And if the impulse is shifted (i.e., delayed), then the function is also delayed.

Convolution is a means to implement a linear filter directly. Convolving a signal with a filter impulse response gives the filtered output. That a filter is linear means that when two signals are added together and fed into it, the output is the same as if each signal had been filtered separately and the outputs then added. together. In other words, the response of a linear system to a sum of signals is the sum of the responses to each individual input signal.

Any linear filter may be represented in the time domain by its impulse response. Any signal x(n) may be represented in the time domain by its impulse response. Any signal x(n) may be regarded as a superposition of impulses at various amplitudes and arrival times (i.e., each sample of x(n) is regarded as an impulse with amplitude x(n) and delay of n). By the superposition principle for linear filters, the filter output is simply the superposition of impulse responses, each having a scale factor and time shift given by the amplitude and timeshift of the corresponding impulse response.²⁵

Each impulse causes the filter to produce an impulse response. If another impulse arrives at the filter's input before the first impulse response has died away, then the impulse response for both impulses is superimposed (added together sample by sample). More generally, since the input is a linear combination of impulses, the output is the same linear combination of impulse responses.²⁶ Fast convolution, (the method used by the CARL convolvesf program) takes advantage of the Fast Fourier Transform (FFT) to reduce the number of calculations necessary to do the convolution.

A Conventional Application: Filtered Speech

The first set of sound examples, IV.OA - C, demonstrates a conventional application of the CARL convolvesf program. Three simple FIR filters are designed via a standard filter-design program, and each, in turn, is applied to the same speech soundfile. The filter-design program, fastfir, expects the user to: specify the number of samples in the impulse response, select one of four filter types (low pass, high pass, band pass, or band reject), specify the window type (e.g., Hamming, Kaiser, etc.), specify the amount of stop band attenuation, and specify the cutoff frequency. All three filters in this series of examples have impulse responses of 4096 samples, use Kaiser windows, and specify a 120dB stop band attenuation at the band edges.

Sound Example IV.OA demonstrates the convolution of a speech soundfile with the impulse response of a low pass filter with a cutoff frequency of 200Hz. Figure 1 is the magnitude o 0 of the Fourier transform of the filter's impulse response.

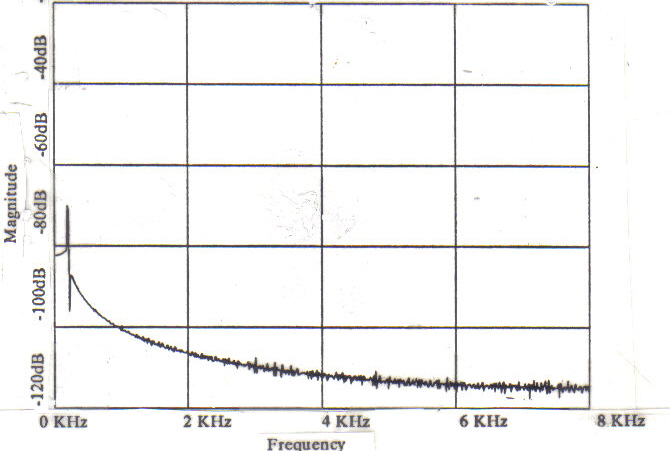
Figure 1: Magnitude of the FFT of the Impulse Response of Filter IV.OA

Sound Example IV.OB demonstrates the convolution of a speech soundfile with the impulse response of a high pass filter with a cutoff frequency of 3kHz. Figure 2 is the magnitude of the Fourier transform of the filter's impulse response.

Figure 2: Magnitude of the FFT of the Impulse Response of Filter IV.OB

Sound Example IV.00 demonstrates the convolution of a speech soundfile with the impulse response of a bandpass filter with a cutoff frequencies at 400 and 700Hz. Figure 3 is the magnitude of the Fourier transform of the filter's impulse response.

Figure 3: Magnitude of the FFT of the Impulse Response of Filter IV.00

There are numerous musical applications of non-time-varying filters such as these. One such subset comes under the general heading "equalization." In recording engineer terminology, filters such as these provide control of the "presence," "brilliance," "smoothness," "muddiness," "boominess," etc., of a recording or broadcast via simple large scale re-adjustment of its relative spectral levels. Another class of musical applications comes under the general heading "noise suppression." Simple filters as these have often been used to remove unwanted "hiss" and "hum" from less than optimal location and studio recordings.

As concerns the general focus of this article (i.e., transforming speech into music), it is clear that a wide variety of unique filters might be so designed and the spoken text transformed via its convolution with their impulse responses. However, what is more interesting and significant are the musical possibilities of using impulse responses other than those produced via standard filter-design programs.

A New Application: Reverberation

To date, the only suggested musical application for fast convolution (other than as an efficient means of implementing FIR filters) has been as an unusual technique for artificial reverberation. Via convolution, it is possible to generate the ambiance of any room and to place any sound within that room. This is done by convolving an arbitrary input with the impulse response of the desired room. For example, if the desired musical goal is to have one's violin piece played in Carnegie Hall, all that is necessary is to convolve a digitized recording of the piece with the digitized impulse response of Carnegie Hall. This is exactly what Moorer and a team of researchers from IRCAM were exploring when they made a "striking discovery^- regarding the simulation of natural-sounding room impulse responses.

Moorer and his team collected the impulse responses from concert halls around the world for study. While digitizing them, they "kept noticing that the responses in the finest concert halls sounded remarkably similar to white noise with an exponential envelope.^"27 To test their observation, they generated synthetic impulse responses with exponential decays and then convolved them with a variety of unreverberated musical sources. Moorer reported that the results were "astonishing" and suggested a number of extensions to this technique. Ultimately, though, Moorer dismissed this reverberation method because of the "enormous amount of computation involved" (Moorer used direct convolution), and because of the fact that, "even via fast convolution," real-time operation was "still more than a factor of ten away for even the fastest commercially available signal processors.^- However, when the concern is "musical potential" as opposed to "real-time potential," fast convolution of speech with exponentially decaying white noise proves to be a rich source of new musical effects.

Sound Examples IV.1A and B demonstrate the convolution of a speech soundfile with two synthetic rooms consisting of single impulses followed by exponentially decaying white noise. The only difference between the two is the length of their "tails." The first is 1.9 seconds, and the second is 3.9 seconds. Both of these examples (IV.1A and B) confirm that a synthetic impulse response composed of exponentially decaying white noise produces an extremely "natural sounding" and "uncolored" "room." They also clearly demonstrate that reverberation via fast convolution of a synthetic room response is a powerful tool for computer music. Obviously, a "clean" and controllable reverberator such as this has numerous musical applications, particularly in the area of record production.

Sound Example IV.1C is the cmusic realization of another Moorer suggestion. He notes that by "selectively filtering the impulse response before convolution, one could control the rolloff rates at various frequencies" and thereby produce highly ^-coloredrooms.²⁸ In this example speech is convolved with a synthetic room consisting of a single impulse followed by 2.9 seconds of exponentially decaying, band-limited white noise. In the score the NOISEBAND argument has been set to 3KHz, and the sound result is quite muted - a ^-low-pass filtered" room.

Within the cmusic software synthesis environment, it was quite simple to design a model score which allowed the user to "tailor" the room to a wide range of musical needs. This score model provided software "knobs" for the direct specification of DRYAMP (direct signal), WETAMP (reverberated signal), NOISEBAND (i.e., tone), and DECAY-LENGTH. Admittedly, all four of these controls are found on every moderately priced reverb unit, and each is mentioned by Moorer as being directly applicable in just this context. However, a musically significant control included in the model score above, and to date, missing from all analog and most digital reverberators (and which seems to have been ignored by the Moorer team as well), allows the SLOPE of the decay to be arbitrarily controlled. As it turns out, this is the key to creating a whole new class of "spaces" -merely by convolving sources with synthetic rooms which have other than exponential slopes.

The following two sound examples illustrate this new effect. Sound Example IV.1D demonstrates the fast convolution of speech with a room response composed of logarithmically decaying white noise. The resultant ^-space^- is far less ^-roomlike^- than it is ^-cloudlike.^- Thus, I call rooms such as these "cloud rooms."

Another unique class of "rooms" results from the fast convolution of an arbitrary input with exponentially increasing white noise. Sound Example IV.1E is such a room. In this example, it is quite interesting how the spoken text is smeared by the process, almost sounding as if it was played backwards. The room impulse response is 3.9 seconds in duration, and the noise noise ramps up from silence to - 24dB below the level of the initial impulse. I refer to rooms of this type as ^-inverse rooms.-

Sound Examples IV.1A - E show how convolvesf and cmusic can be used to design and implementing a wide variety of synthetic performance "spaces." The possibilities range from extremely "natural sounding" rooms to some truly unique ones - rooms, for example, in which the apparent intensity of the source grows rather than fades. Although in the eyes of a recording engineer a highly colored room might be quite undesirable, to a composer, it may provide just the necessary means by which certain sound structures can be differentiated. An "uncolored" room response is merely one point in a musically valid sound continuum.

Furthermore, the simple addition of a decay-slope control to the standard set of reverberator controls has been shown to create a unique and wide ranging set of new musical possibilities. In the case of (logarithmically decaying) "cloud rooms" or (exponentially increasing) "inverse rooms" the "basic" reverberator is turned into a powerful new transformational tool.

A New Way To Combine Musical Sounds: Generalized Resonators

Clearly, a number of significant new musical applications result from simply extending the current use and understanding of convolution (e.g., "cloud rooms," and "inverse rooms"). In addition to this, however, the convolution process can provide a totally new way to combine musical sounds.

In the case of filtering, the impulse response of a desired filter is produced with the aid of a basic filter-design program. In the case of reverberation, the impulse response of any "room" can be produced by synthesizing noise of varying "colors" and decay-slopes. However these are not the only forms of digital signals which can serve as impulse response. Via convolution, any sound can be thought of as a "room" or "resonator." This has always been known by those who have understood the convolution process, yet, to this point in time, the musical significance of this simple fact has gone largely unexplored. (of what use is a filter which rattles like a tambourine to a recording engineer who's main concern is the 60Hz hum in his control room?)

But just as it is possible to play one's violin piece in Carnegie Hall by convolving it with the hall's impulse response, so too is it possible to play that same piece inside a suspended cymbal by convolving it with the sound of a suspended cymbal. For, as was noted in the introduction of this article, the only difference between Carnegie Hall and the suspended cymbal (besides the seating) is that, acoustically, they are manifestations of two slightly different filters.

Convolution provides a more general means by which speech can be infused with pitch. Since it is possible, via convolution, to combine any two sounds, one need only find a sound with the desired pitch and convolve it with speech. The speech can be infused with the pitch (and timbre) of the "found sound" because the convolution of any two sounds corresponds to their "dynamic spectral intersection.^- Thus, there is only energy in the output at frequencies where both inputs have energy. Since the noise components of speech have energy at all frequencies, the product of the spectral intersection with a pitched "found sound" has a definite pitch.

Convolution is more generalized than the ^-string-resonator." The Karplus-Strong plucked-string algorithm is merely a difference equation which, due to the recursion relation, happens to efficiently produce a musically interesting impulse response. But the resulting sound is always "string-like." Convolution literally provides the ^composer/sound-designer with an orchestra of pitch infusers, both harmonic and enharmonic. Moreover, the filter (i.e., impulse response) can have musical meaning.

With respect to real-time implementation, the advantage of the ^-string-resonatoris that it is a one-step process and very computationally efficient. On the other hand, convolution is a two step process: (1) find or design the impulse response, (2) convolve it with the source. Furthermore, convolution (even fast convolution) is very computationally intensive. Also, in the case of fast convolution, there is an inherent block-delay due to the fact that an entire FFT-buffer of input must be collected before any output can be produced. Thus, the techniques which follow are inherently non-realtime.

The musical model which most closely resembles the use of the Karplus-Strong plucked-string algorithm as a resonator is that of someone shouting into a piano with the sostenuto pedal depressed. Convolution takes this musical practice several steps further. Via convolution, it is possible to "speak from within" bassoons, violins, cymbals, orchestras, and even other voices.

It is important to note that the musical utility of convolution is not limited to finding the "right" sounds. Actually, it is the combination of controllability and variety which make convolution so musically significant. Three possibilities exist as regards the "ideal resonator:" (1) find the "right" sound, (2) modify the "found sound," or (3) synthesize the sound "right."

Any "found sound" can be made into the ^-right^- sound. Given a phase vocoder and a software synthesis environment such as cmusic, this operation is fairly straightforward. For example, suppose the structural mandate of the compositional process requires that a specific spoken word be infused with the timbre of an antique cymbal, but the pitch of the cymbal is too high for an effective spectral intersection. With the phase vocoder it is a simple matter to independently time-compress or pitch-transpose the sound to the exact frequency which is required.

It is also a- simple matter to synthesize a sound with the spectral characteristics which satisfies the compositional imperative (which is exactly how the reverberation examples were done). For example, if the compositional necessity is to infuse speech with the sound of a plucked-string, one can synthesize the sound of a plucked-string (possibly by using the Karplus-Strong plucked-string algorithm) and convolve the speech with it. In fact it is actually possible to deduce whether a given "found sound" is the "right" soundfor a particular application by understanding the way in which the sound will function as an impulse response.

There are four aspects of the impulse response which offer the user direct control over the characteristic of the resulting spectral intersection. These four aspects are, (1) the relative level of the initial sample (2) the character of a single period, (3) the overall temporal envelope, and (4) the extent to which the response is composed of discrete perceptual events.

The relative level of the initial impulse sample determines the amount of "direct" signal present in the output. Just as with the reverberation examples demonstrated previously, the initial impulse sample is the means of controlling the relative mix between the direct and "filtered" sound. It is a simple matter to add a gain-adjusted, single impulse to the beginning of any "found sound," and to thereby produce the desired balance between the source and "resonance."

The character of a single period (at least for pitched impulse responses) corresponds with the degree of "reverberance." A pitched "found sound," with only an isolated peak per period (as shown in Figure 4) will typically infuse the speech only with a specific pitch. On the other hand, a sound (such as that in Figure 5) with many comparably-sized peaks per period will both, infuse the speech with pitch, and also infuse the speech with other general attributes as well. Typically, the two individual components (i.e., speech and pitched "found sound"), retain more of their own identities. In this case, the speech is not merely infused with pitch. Rather, the spectral intersection is more akin to speech coming from within some "object" which is highly "colored" with a certain pitch.

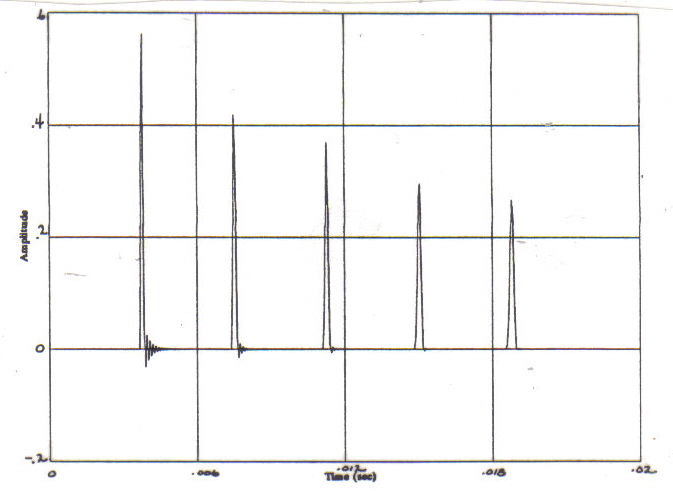
Figure 4: A sound with an isolated peak per period

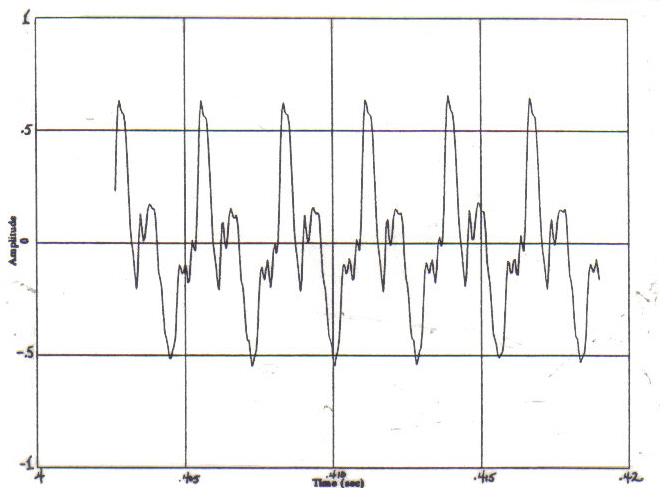
Figure 5: A sound with many comparably sized peaks per period

Another control over ^-reverberance^- is the time-domain envelope. "Found sounds" with exponentially decaying time-domain envelopes will generally result in a reverberant quality. Obviously, one can apply an exponential envelope to any "found sound" to control its relative "reverberance." From the macroscopic level, one can shape a "found sound" by imposing any imaginable temporal envelope to produce a variety of musical results: from the microscopic level, one can effect a similar general transformation by mixing in, or filtering out, various amounts of noise (this is one musical situation where a "noisy" source recording may be "better" than a quiet one).

A different kind of control can be obtained by "slowing down" the spectral evolution of the "found sound" by time-expanding it via the phase vocoder. In this way the impulse response of a rapidly varying filter can be transformed into a slowly varying one.

Lastly, if the pitch of the impulse response is fixed, the degree of spectral intersection can be determined simply by the duration of the impulse response. In general, the shorter the impulse response is, the wider the spectral bandwidths of the resonant peaks are. In a hypothetical case where the impulse response is restricted to being a strictly periodic impulse train, the bandwidth can be directly related to the duration of the impulse response by the following equation:

BW= 1/T

where BW is the bandwidth of the spectral peaks, and T is the duration of the impulse response. If, for example, the impulse response is 4 seconds long, the spectral bandwidth at each spectral component of the pulse train is the .25Hz. Thus by synthesizing a pulse train of the proper frequency and determining the proper duration of the impulse response file, one has control over the degree of spectral intersection.

The following seven sound examples are convolutions of speech with a variety of pitched resonators; they serve to demonstrate the basic operation and control of this new technique. These examples include: marimba, cowbell, antique cymbal, violin, orchestra, processed orchestra, and a synthetic tone. In each case, the result of the spectral intersection is the infusion of the speech with the pitch and the general attributes of the resonator.

The first sound example, IV.2A, demonstrates the convolution of speech with a digitized and denoised recording of a marimba. Its. pitch, A₂ (110HZ), was produced by striking the wooden bar on the instrument with a medium-hard yarn-wound mallet. The following five figures illustrate the time-domain and frequency-domain characteristics and the spectral intersection of the speech and marimba waveforms. The resulting sound can be understood by the observable characteristics of the "resonator" (i.e., the marimba). The speech is clearly infused with both the marimba's pitch and timbre. This spectral intersection is also characterized by the reverberant percept associated with exponentially decaying time-domain envelopes. The speaker sounds as if he is talking from within some tiny "highly-colored" room. The color of this "marimba-room" can be explained by its FFT which shows no significant spectral energy above 1kHz (Figure 22). Thus, a spectral intersection between speech and this specific "marimba-filter" results in the attenuation of all frequencies above 1kHz.

The second sound example, IV.2B, demonstrates the convolution of speech with a digitized and denoised recording of a cowbell. Its pitch, E₃ (164.81Hz), was produced by striking the metal edge with a triangle beater. Like the marimba, the time-domain characteristics of this 2.6 second "found sound" are a sharp attack and an exponentially decaying envelope.

The general behavior of the "cowbell resonator" is quite similar to that of the "marimba resonator." This can be explained by the common characteristics of their time domain waveforms (i.e., a nearly instantaneous onset and an exponentially decaying envelope). In the spectral domain it is clear that they are filters with very different frequency responses. The "cowbell resonator" has a much broader spectrum than the marimba and more components in common with the voice, particularly in the high register. Where the "marimba-filter" had an effective cutoff frequency of 1kHz, the "cowbell-filter" passes frequencies slightly higher than 4kHz. The "cowbell-resonator" like the marimba, infuses the voice with its pitch and timbre. However, the sound of this particular intersection (cowbell and voice) consists of two components, a high pitched ringing associated with the metallic attack (i.e., the clang tone), and a lower pitched ambiance associated with the cavity of the bell. This intersection sounds like the metal triangle beater is being ^"scraped" across the rim of the cowbell in some irregular rhythm. What is musically significant is that the rhythm of the "scraping" correspond to the time-varying spectral information in the input signal.

The third sound example, IV.2C, is actually three examples in one. It demonstrates three convolutions of speech with the sound of an antique cymbal. The difference in the three is the length of the impulse response. This example sonically illustrates the relationship between the length of the impulse response and the bandwidth of the peaks in the associated filter. The sound example consists of the three intersections played in succession. The lengths of the impulse responses are 1.9 seconds, .2 seconds, and .05 seconds which corresponds with bandwidths of .5Hz, 5Hz, and 20Hz. The pitch of the antique cymbal, C₇ (2093Hz), was produced by striking the edge with a metal triangle beater.

It is interesting to note the dramatic difference in sound which results from altering the bandwidth of the resonant peaks via the length of the impulse response. In the first case (impulse response of 1.9 seconds) the "antique-cymbal-filter" simply rings. Almost all the frequency components of the speech are nulled. The few additional articulations are actually re-initializations of the ^-filter" by either impulses which follow long silences (such as that following the pause between the end of the title and the start of the author's name), or by high-amplitude, high-frequency components of the text (such as the "ch" in the word ^-Archibald,^- and the "sh" in the word "MacLeish").

As the bandwidth of the peaks increases, the text becomes more predominant. Also, since less of the total time-domain waveform is being used (i.e., less exponentially decaying envelope) the sound exhibits progressively less "reverberance." The sound of the final intersection (impulse response of .05 seconds) is more highly ^-fused^- with the ^-resonator." It is as if the "antique-cymbal-filter" is "gated" by each syllable. This is quite different from the result of the first intersection in which it sounds as if the antique cymbal is being ^-triggered" or "struck" by certain features of the waveform.

Another point to note regarding this sound example has to do with the low-frequency component resulting from the poor recording conditions. No matter what the cause, the effect of this 60Hz tone on the sound result is quite significant. Actually, it represents one of this technique's more powerful controls. Given an antique cymbal without this low-frequency component, one could simply mix in a sine tone of the desired frequency and amplitude. The amplitude of this added sine tone would control the spectral dominance at that frequency. The combination of controllable bandwidth (via the length of the impulse response) and the ability to bring out any desired portion of the input spectrum (by mixing sine tones in with the "found sound" at the desired frequencies) prove to be two extremely powerful controls.

Although the above three examples (and the filtering and artificial reverberation examples which preceded them for that matter) have all demonstrated the convolution of speech with "resonators" composed of single events with nearly instantaneous onsets (i.e., a single impulse or strike), it is also possible to convolve speech with sounds which are not so characterized. The fourth sound example, IV.2D, is just such a case. It demonstrates the convolution of speech with the sound of a bowed violin string. I call this effect ^-bowed-speech." The resonator consists of the first 300 milliseconds of a bowed violin tone (which corresponds to a bandwidth of 3.3Hz at each of the harmonics). The pitch, D4 (293.66Hz), was produced by bowing an open string (obviously without vibrato). The following two figures show the spectrum of the "resonator" and the spectral intersection with speech. Besides the unique sound result it is interesting to note how the formant structure of the speech is preserved in this intersection in a way that it has not been in any of the previous intersections. This can be explained by the fact that both the vocal and the violin resonators have formant regions around 2300Hz.

The musical application of fast convolution is not restricted to single-pitched resonators. It is also possible to convolve speech with chords and with extremely complex contrapuntal musical textures. In this regard, the fifth sound example, IV.2E, demonstrates the convolution of speech with a digitized and denoised recording of an orchestral performance. The excerpt was taken from a stereo LP recording of Bernstein conducting the Ives Unanswered Question with the New York Philharmonic Orchestra. The specific musical passage is from the second flute and string entrance. The 2.3 second impulse response is taken from the very end of the phrase and is characterized by an exponentially decaying envelope. The strings are sustaining a chord while the flutes play an ascending minor third above. What is musically significant about this example is the way that the musical structure of the Ives passage, which serves as the ^-resonator,^- is transformed by the timing and spectral character of the input speech. Different segments of the text ^-play^- the excerpt differently.

The sixth sound example, IV.2F, employs another portion of this same passage from the Ives Unanswered Question. However, this ^-resonator^- has been preprocessed using a phase vocoder to modify the "found sound" into the "right sound" (i.e., to either improve the spectral alignment of the two or, as in this case, to ^-tune' the resonator to some specific frequency and spectral envelope). This ^-resonator^- is time-expanded by a factor of 10 and the pitch is transposed down by two octaves. The duration of the impulse response is .13 seconds.

So far, all of the pitched resonators which have been convolved with speech have been straight or preprocessed "found sounds." However, it is also possible to synthesize the sound of the resonator directly. Actually, this is exactly how the reverberation examples were generated (i.e., by convolving speech with synthetically generated white noise). But in that case the sound which was synthesized was unpitched. The sound of the resonator was generated using the cmusic fltdelay unit-generator and has the now-familiar timbre of a Karplus-^'Strong plucked-string. The pitch is C₄ (261.65Hz), and the duration of the impulse response is 1 second. Like the previous percussion "resonators," the time-domain characteristics of this "string-resonator" are a sharp attack and an exponentially decaying envelope. The following two figures show the plucked-string's spectral characteristics and the result of the spectral intersection.

The two musically significant results demonstrated by all seven of these sound examples are, (1) that the convolution of speech with a pitched sound will infuse the speech with the sound's pitch and, (2) that the speech will also be infused with the timbre of the pitched sound. Considering that two of the fundamental aspects of the composition process are the structuring of pitch in time and the orchestration of that pitch structure, fast convolution provides a powerful new tool. Not only is it possible to infuse speech with the pitch and timbre of single isolated musical sounds, but it has also been shown that, via convolution, one can infuse speech with sounds of any degree of musical or sonic complexity. Any sound can be a "resonator" of any other sound. Although this has been theoretically possible since the invention of convolution, the technique has never been employed for this purpose. For many years, such an application was not technologically feasible. More recently, however, feasibility has not been an issue. Rather, the musical significance of this application has simply not previously been recognized.

The generality of fast convolution of soundfiles means that any signal can be an excitation and any signal can be a resonator. Given this basic fact, the contemporary practice of devising unique acoustical resonators and equally unique modes of excitation can now be viewed as a special case among a wide range of possibilities. Via convolution it is not only possible to speak in Carnegie Hall or in a synthetic concert space of any size or coloration, but - as shown above - it is now possible to speak within a room which is not a room at all, but rather, a violin, a section of violins, or a section of violins playing passages from Beethoven's Fifth Symphony.

In the case of speech convolved with Beethoven the result is similar to the ^-talking-orchestra^- effects produced by Moorer (Perfect Days) and others using linear predictive-coding (LPC) techniques. However, there is a significant difference between an LPC "talking-orchestra" and a fast convolution "talking orchestra." LPC is an analysis/synthesis procedure. Typically, the LPC resynthesis of voiced speech is done with a pulse train as the excitation signal. For LPC "talking orchestra" effects, the pulse train is replaced by the orchestra (or flute, as in the case of the Moorer). This orchestral excitation signal is then filtered by a time-varying filter which mimics the time-varying formants (resonances) of the vocal tract. Thus, in the case of the LPC "talking orchestra" the analyzed behavior of the formants modifies the spectrum of the music. However, it does not alter the music itself in any significant way.

The fast convolution "talking orchestra" is managing something totally different and much more significant musically. In the "talking-orchestra" effects produced via convolution, the musical excerpt is actually "played" by the spectral characteristics of the speech. Its musical structure is effectively re-organized by the input. Thus, the fast convolution of speech with musical excerpts can be viewed not merely as a ^-signal-processing^- technique, but rather as a "music-processing" technique.

As our understanding of the compositional process, and the mechanisms of perceptual organization, becomes correlated with our understanding of physical systems, and as these continue to inform and be informed by man's creative application of computer technology, "music processing" will increasingly become the fundamental issue. Perceptually, fast convolution is an example of a sophisticated "music processor." The musical potential of a tool with this level of interdependence and control is tremendous. It should be worthy of further investigation for some time to come.

The Convolution of Speech with Enharmonic Timbres

All the resonators employed in the seven previous sound examples were highly pitched. However, it is possible to convolve speech with any sound. The following three sound examples convolve speech with the sounds of percussion instruments to which pitch is not normally ascribed - snare drum, tom-tom, and suspended cymbal.

The first sound example, IV.3A, demonstrates the convolution of speech with a digitized recording of a snare drum. The sound of the drum was produced with a single stroke of a medium-wood drum stick. The snares were turned off. The spectrum of the drum is noise-like and the envelope is exponentially decaying. Thus the sound result of the intersection is "room-like." This is literally an example of someone speaking from within a snare drum.

The second sound example, IV.3A, demonstrates the convolution of speech with a digitized recording of two differently-tuned low tom-toms which were struck virtually simultaneously. The sound was produced with two medium-hard yarn-wound mallets. The duration of the impulse response is 3.9 seconds. Although the time-domain characteristics of this resonator, like the snare drum, feature a sharp attack and an exponentially decaying envelope, the result of this spectral intersection is quite different. Whereas with the snare drum the sound was "room-like," with the tom-toms the spectrum of the speech is both modified and active in the articulation of a rhythmic pattern which is based on its impulsive character. With such a long impulse response the "tom-tom room,^- like the previous example which used an antique-cymbal, will simply "ring." Thus, the rhythmic pattern, which is primarily derived from the rhythm of the words, which, in effect, strike the tom-tom at the outset of each. In this example the words are also mallets.

The third sound example, IV.3C, demonstrates the convolution of speech with the sound of a digitally recorded fourteen-inch suspended cymbal. The sound was produced using a soft yarn-wound mallet. The duration of the impulse response is 3.9 seconds. The result of the intersection is a two-component percept: a bright high "sparkling" resonance associated with the attack and a low ringing drone associated with the decay portion of the sound. What is most interesting about this example is the way that the varying spectrum of the voice corresponds to the sound of mallets randomly moving along the surface of the cymbal from the edge to the center. Typically as the cymbal is struck closer to the center or "crown," the timbre is brighter and the decay shorter. Also, this example is so "effective" because the spectra of the cymbal is so broadband that while there is a great deal of interaction between the two spectra there are very few significant "nulls." The following two figures illustrate the spectral characteristics of the cymbal and the result of its spectral intersection with the speech.

There is no difference between pitched or unpitched resonators with regard to convolution itself. Thus, whereas the "string-resonator" could only infuse speech with harmonic string timbres, fast convolution can infuse speech with any timbre. Obviously this represents a significant advance in the general musical utility of this powerful new tool.

The examples of convolution with percussion instruments or unpitched instruments included herein represent extensions of a now conventional avante-garde musical practice. Generalized resonators via fast convolution of soundfiles represents the mechanism by which the full musical potential of what I call "transformational resonance" can be realized.

The Convolution of Speech with Speech

To this point speech has been convolved with both harmonic and enharmonic spectra from ^-found,^- ^-modified-found,^- and "synthesized" sounds. But, there is yet another class of "found sounds" with which convolution can be utilized. The sounds in this class are themselves speech sounds. Convolving speech with speech produces some highly original results. I call this general class of intersections "twice-filtered-speech."

The most important feature of "twice-filtered-speech" is that the component spectra have both a musical and a literal "meaning." What new levels of spectral meaning emerge from a spectral intersection such as this? What new semantic meaning emerges? These are clearly questions of psychological significance which will require a great deal of further research. The present research demonstrates a technique by which a psychoacoustic investigation on this subject may be pursued.

In this section speech is convolved with speech of varying degrees of complexity. Two of the examples demonstrate speech convolved with a single word and a phrase. The other three sound examples demonstrate speech convolved with the sound of laughter and the sound of crying which is time-expanded using a phase vocoder. The final sound example demonstrates one of the more powerful controls of the technique, a control over the "direct/mix" level of the input signal.

The first sound example, IV.4A, demonstrates the convolution of speech (i.e., the title of the poem) with the single spoken word "there." The duration of the impulse response is .44 seconds. The result of this intersection is a very complex one. Clearly several repetitions of the ^-there-filter^- are distinguishable. If one merely focuses attention on the quality of the "twice-filtered" result, its sound is quite mangled, as if someone is speaking with cotton in their mouth.

The second sound example, IV.4B, demonstrates the convolution of a speech soundfile with a spoken phrase. The specific phrase has a duration of 2.4 seconds. Actually it is the same sequence of words as the input, but the voice is that of a three year old boy. In this "twice-filtered-speech" one can clearly distinguish two separate voices, and some of the "room's" text. It is difficult to make out any of the words of the input text.

The third sound example, IV.4C, demonstrates the convolution of a speech soundfile with the single laugh of a 4 month old infant. The duration of the impulse response is 1.4 seconds. The result of this intersection is quite amusing in that the input speech "plays" the "room" and in so doing creates a string of laughter from the single laugh. This is an interesting example because, if one is simply listening to the transformation of the input file, the laugh is difficult to perceive. When concentrating on the source, the "laughing-room" merely sounds like a bubbling surface. However, if the listener is told to listen for laughter, it becomes very clear. To provide the listener with more time to resolve this fairly complex percept, the input is both the title and the first line of the text.

The final sound example, IV.4D, consists of two convolutions which have been joined together to demonstrate, side by side, one of this techniques more powerful controls, the ability to control the "direct/mix" balance of the resulting intersection. This control is achieved quite simply by adding a single, gain adjusted impulse to the onset of the "room." Just as in the artificial reverberation examples, the level of this initial impulse corresponds to the level of direct signal.

Both sections of Sound Example IV.4D are convolved with a fragment of a child's cry which is time-expanded by a factor of 11. The length of the impulse response is 3.9 seconds. The only difference between the two is that an impulse has been added to the beginning of the "crying-room" in the second section. The spoken text is made plain by the added impulse. The sound result of this specific "twice-filtered-speech" example can be explained by the exponentially increasing time-domain envelope which, as had been previously shown in the reverberation examples, results in a "smearing" of the speech input and an almost backward sound effect.

"Twice-filtered-speech" is not the only way that effects such as these can be achieved. Just as an orchestral excerpt can be substituted for the excitation signal in LPC, so too could speech be substituted. Musically, the complex percept which results from the dynamic spectral intersection of two speech soundfiles can be compared with the some of the complex speech-sounds in Stockhausen's Gesang de Junglinge or Berio's Thema (Omaggio a Joyce). However, in these two compositions there is no true intersection of the texts, but rather, a fragmentation and juxtaposition of phonemes. "Twice-filtered-speech" uncovers a language somewhere between the two component spectra, a language which interleaves the two spectra in a fundamentally new way.

Convolving Speech with Complex Resonators

It is also possible to convolve speech with multi-event sounds. I call such sounds "complex resonators." In general, if a "sound-object" is perceived as being composed of a number of sound events, the result of the convolution with such a sound-object will be composed of a similar number of events, around which the input is copied. These copies are perceived as "echoes" of the input. In this section, speech is convolved with several "complex found" and several "complex synthesized" resonators. The results of these spectral intersections are equally complex and of great musical potential.

The first sound example, IV.5A, demonstrates the convolution of speech with a cowbell arpeggio. The duration of the impulse response is .94 seconds. The structure of the impulse response reveals a very complex pattern; however, each of the most prominent peaks corresponds with a clear repetition of the input.

The second sound example, IV.5A, demonstrates the convolution of speech with a sound which is a composite of a number of the "simple resonators" used previously. I call this resonator the "kitchen sink." The cmusic score used to mix the components of this complex resonator" is given below. All of the acoustic instrument sounds are given by name. The instrument "tail," which produces exponentially decaying white noise, is used to effectively "blend" the varied components by adding a faint "reverberance."

The third sound example, IV.5C, demonstrates the convolution of speech with the same complex resonator as above (the "kitchen sink"). The only difference is that an exponentially decaying envelope has been applied to the entire soundfile. The effect of this "control envelope" is that the now exponentially decaying impulse response is more like that of a real room (i.e., the energy of the input is dissipated more evenly). I call this resonator the "fading sink."

The degree of control gained by the simple addition of an amplitude envelope is quite clear when one compares the spectral intersection of the "fading sink" with that of the "kitchen sink." Envelope control of "complex resonators" considerably increases their musical utility. By simply applying an exponential envelope to any "complex resonator" the proportional structure and characteristic components of that resonator's unique structure can be maintained while, at the same time, the resonator can be made to more closely emulate the natural behavior of real acoustic spaces, and to thereby serve in a larger number of conventional applications.

Now, for example, it is possible to actually "compose" the space for the performance of one's music as well as composing the music itself. One can coordinate the instrumentation of a chamber work, for example, with the resonance in the "room," like matching the furniture to the wallpaper and carpet. Obviously, one can also tune the instruments so as to harmonically relate the performance space to the harmonic structure of the music. The possibility to tune both the timbre and the resonant frequencies of an artificial performance space is a clear extension of the "chord space" idea suggested in the previous "string resonator" applications.

The following four sound examples demonstrate a way in which the echo pattern and the echo density can be controlled by specifying the desired sequence of impulses directly. A number of new and potentially significant musical applications emerge from this simple demonstration.

Sound Example IV.5D demonstrates the convolution of speech with a synthesized "complex resonator" consisting of 4 equally spaced impulses of decreasing amplitude. The duration of the impulse response is 3 seconds. This is an example of simple "echo."

Sound Example IV.5E demonstrates the convolution of speech with a synthesized "complex resonator" consisting of 4 equally spaced impulses of increasing amplitude. The cmusic score is exactly the same as above except that the notelist is reversed. This is an example of what I call "reverse echo."

Sound Example IV.5F demonstrates the convolution of speech with a synthesized "complex resonator" consisting of 14 impulses whose amplitudes and timings have been explicitly defined to be non-periodic. The duration of the impulse response is 3.9 seconds. This is an example of what I call "composed echo." This "composed echo" technique is one of great musical potential. It makes possible the structuring of a composition on a whole new level by underscoring or infusing it with structurally significant rhythmic motives.

Sound Example IV.5G demonstrates the convolution of speech with a synthesized "complex resonator" which consists of 30 impulses whose start-time and amplitude are selected at random. The duration of the impulse response is 3.77 seconds. This is an example of what I call "random echo." Due to the close succession of some of the impulses in this example the percept changes from a sequence of discrete copies of the input to a more general "reverberance."

"Reverse echo," "composed echo," and "random echo" represent extensions of convolving speech with complex resonators. Musicians have expressed frustration with the fixed repetition rate of traditional analog and digital echo devices. Clearly these extensions represent possible new solutions.

The three previous sound examples demonstrate simple applications of three new echo" techniques. A more complex application of these new techniques is demonstrated in Sound Example IV.5H. Speech is convolved with a synthesized "complex resonator" composed of equally-spaced discrete echo's, and irregularly-spaced and "shaped" reverberant "tails," all placed within a full-duration time-varying complex "tail." The effect is like an Escher drawing - "rooms within rooms within rooms within rooms " The duration of the "master room" is 3.9 seconds.

Figure 6 is a plot of the shape of the first "tail," the "master room." Its function in this truly "complex resonator" is the generation of a continuously varying background resonance within which the smaller "rooms" are placed. A "room" resonance of this sort would be highly unlikely in the real world.

Figure 6: Plot of the "Master Room" Response of IV.5H

Figure 7 is a plot of the total impulse response of resonator IV.5H. In this figure the two components (i.e., impulses and tails), and the various shapes of the inner "rooms" are clearly discernible.

The degree of independence demonstrated through the design and execution of this sound example is truly unique. There exist no current technology which would allow for the composition of artificial rooms with such a degree of "controlled complexity." Not only is it possible to "find," "modify," and "control" complex resonators, but, as has been shown, it is also possible to design arbitrarily complex "rooms" by assembling and mixing fragments of "found sounds" or by directly composing the desired patterns of impulses and shaped noise.

Convolving Rooms with Speech: Commutation

In some cases it is not clear whether the input is being repeated or the impulse response is. Two conditions contribute to this effect, (1) the impulse response is characterized by more than one event, and (2) the events in the impulse response are "musically meaningful." If the events in the impulse response are not musically meaningful (i.e., they are effectively scattered impulses), the result will be similar to the input being "echoed" (i.e., copied at each impulse). However, if the impulse is something musically meaningful, like the opening motive to Beethoven's 5th Symphony, it will be unclear whether or not the speech is being "echoed" four times or whether the four-note musical motive is being "triggered" by each strongly impulsive event in the speech. This perceptual ambiguity or "illusion" is due to the commutative nature of the convolution operation. I call it the "commutation illusion."

Once it has been clearly articulated, an artistic question points to an infinite number of "correct" solutions. In this particular case the goal was to investigate how speech might be digitally transfigured into musical sound. The immediate solution was the discovery of a new and potentially powerful set of tools; the ultimate solution will be their musical manifestation in the form of a composition.

Musical innovation is not merely the story of "correct" solutions but rather the ^"innovative application" of a limited set of musically " valid" solutions. Each " tool" (solution) brings its own perspective to bear on the task at hand. And thus, even when the results of its application appear the "same" - on the surface, the means can, and often do, point to entirely different ends.

Two new tools for music have herein been presented. One is a technique for infusing speech with pitched string timbres. The other is a technique for infusing speech with any pitched or non-pitched timbre. Both are powerful in that they provide the composer/sonic-designer with a plethora of transfigurational possibilities. Their true significance, and the source of their power, however, is without a doubt the accessibility, in the broadest sense, of their controls.

Bibliography

Bernstein, Leonard. The Unanswered Question: Six ,Talks at Harvard. Cambridge: Harvard University Press, 1976.

Clynes, Manfred. Music, Mind, and Brain. New York: Plenum Press, 1983.

Cope, David H. New Directions In Music. Iowa: Wm. C. Brown Co., 1976.

Dolson, Mark. "The Phase Vocoder: A Tutorial." The CARL Startup Kit. California: Center for Music Experiment. 1985.

Gagne, Cole., and Caras, Tracy. Sound pieces: Interviews with American Composers New Jersey: The Scarecrow Press, Inc., 1982.

Grout, Donald Jay. A History of Western Music. New York: W.W. Norton and Co., 1973.

Jaffe, David., and Smith, Julius. "Extensions of the Karplus-Strong Plucked-String Algorithm." Computer Music Journal. Vol. 7, No. 2, 1983. pp. 56 - 69.

Karplus, Kevin., and Strong, Alex. "Digital Synthesis of Plucked-String and Drum Timbres... Computer Music Journal, Vol.7, No. 2, 1983. pp. 43 - 55.

Kavasch, Deborah. "An Introduction to Extended Vocal Techniques: Some Compositional Aspects and Performance Techniques... ex tempore Vol. 3, No. 1, 1984.

La Rue, Jan. Guidelines For Style Analysis. New York: Norton, 1970.

Moore, Brian C.J. An Introduction to the Psychology of Hearing. New York: Academic Press Inc., 1982.

Moore, F. Richard. "An Introduction to the Mathematics of Digital Signal Processing.- Computer Music Journal, Vol. II, No. 2, pp. 38 - 60.

Moorer, James A. "About This Reverberation Business.^- Computer Music Journal, Vol. 3, No. 2, pp. 13 - 28.

Moorer, James A. "Signal Processing Aspects of Computer Music - A Survey." Computer Music Journal, Feb. 1977, pp. 4 - 37.

Moorer, James A. "The Use of Linear Prediction of Speech in Computer Music Applications." Journal of The Audio Engineering Society, Vol. 27, No. 3, March 1979, pp. 134 - 140.

Pribram, Karl H. ^-Brain Mechanisms in Music: Prolegomena for a Theory of the Meaning of Meaning.^- Music, Mind, and Brain: The Neuropsychology of Music. edited by Manfred Clynes. New York: Plenum Press 1983. pp. 21 - 35.

Risset, Jean-Claude., Wessel, David L. "Exploration of Timbre by Analysis and Synthesis.^- The Psychology of Music. edited by Diana Deutsch. New York: Academic Press, 1982. pp. 25 - 58.

Roederer, Juan G. Introduction to the Physics and Psychophysics of Music. New York: Springer-Verlag New York Inc., 1975.

Salzer, Felix. Structural Hearing. New York: Dover, 1962.

Smith, Julius Orion, "Introduction to Digital Filter Theory," Center for Computer Research in Music and Acoustics, Stanford University, 1981.

Yeston, Maury, ed. Readings in Schenker Analysis and Other Approaches. New Haven: Yale University Press, 1977.

¹This paper was extracted from the author's unpublished doctoral dissertation entitled "The Transformation of Speech into Music", UCSD, 1985.

²Stanley, Dougherty, and Dougherty (1984) and Rabiner, and Schafer (1978).

³ Grout (1973) and Scholes (1970).

⁴Grout (1973).

⁵Bernstein (1976).

⁶ See Pribram in Clynes (1983) p. 25.

⁷ Moore (1982) pp. 229-230.

⁸ Dodge in Gagne and Caras (1982) p. 148.

⁹Moorer (1979) p. 134.

¹⁰Moorer (1977) p. 16.

¹¹Risset and Wessel in Deutsch (1982) p. 36.

¹² Dolson (1985) The Phase Vocoder: A Tutorial.

¹³ Dolson op. cit.

¹⁴ Karplus and Strong (1983).

¹⁵Primary reference, Roederer (1975) pp. 94-98.

¹⁶ Jaffe and Smith (1983).

¹⁷ For easier reference, the sound examples are referenced here according to their enumeration in

Boulanger's dissertation which corresponds to the enumeration on the sound example cassette.

¹⁸ An excerpt appears on the compact disc recording entitled The Digital Domain (1983).

¹⁹ Kavasch (1984).

²⁰ Both were fellows of the Center for Music Experiment during the 1970's and 1980's and both appear on commercially available recordings.

²¹ Also see Yeston (1977), Salzer (1962), and La Rue (1970).

²²Jaffe and Smith (1983) p. 66.

²³ Jaffe and Smith p. 66.

²⁴ See Dolson (1985), Moore (1978), and Smith (1981).

²⁵ Moore (1978) p. 52.

²⁶Smith (1981) p. 25.

²⁷ Moorer (1979), p. 26.

²⁸ Moorer (1979), p. 26.

²⁹ Where * denotes convolution.