INTRODUCTION ISOMETRICS AND THE ORIGINS OF MODAL SYSTEMS: A BRIEF EXPERIMENTAL INQUIRY

Isometrics and the Origins of Modal Systems: A Brief Experimental Inquiry

Tom Amos

Victor Belaiev and Kathleen Schlesinger have posited theories for the origin of modal systems based on the linearly equal placement of finger holes on wind instruments and frets on string instruments. Belaiev calls this technique of placement "metric temperament". Schlesinger calls the technique "isometrics" based upon a passage from Aristotle's Harmonics that is rather problematical in translation. I am using Schlesinger's term merely because hers is from an earlier work and is shorter.¹

Schlesinger's work with the Greek autos led her to the conclusion that the ancient Greek scales could be obtained on that instrument by the equal spacing of six holes below the double reed with further adjustments for the various genera to be accommodated by tuning bands. Her arguments tend to be inconsistent in that she allows certain unequal spacings, and several of the examples of surviving auloi that she presents appear to be directly contradictory to her assertions.²

Belaiev presents a model for the origin of various Soviet ethnic modal systems based on the division of those points which yield fourths, into halves. From these divisions is derived a trichord which Belaiev claims can be used as a model for a pentatonic scale if one overblows the trichord at the fourth (eleventh) or fifth (twelfth). The actual intervals described are a second of 231 cents and a fourth of 498 cents.³ The most obvious weakness of Belaiev's theory is his failure ate a method for arriving at the initial fourths.

J. V. S. Megaw, in his article "Pennywhistles and Prehistory", mentions that the majority of bone fipple-flutes that exist from the Paleolithic have equally spaced holes which seem to correspond to the "natural" lie of the three fingers of the right hand on the flute. He fails to present any measurements of distances, proportions, or frequencies.⁴

Experimental Model

Whatever the shortcomings of the previous studies, there seemed to be some evidence that in some way equal measurements had something to do with scale formation. Inspired by this earlier research, I formulated an experimental model of my own. I wished to discover what scale or patterns would arise if simple fipple-flutes were constructed which had holes bored at points halfway from the front edge of the fipple and the end of the flute, and then two more holes equidistant from the first hole back towards the fipple and also towards the end of the flute, thus:

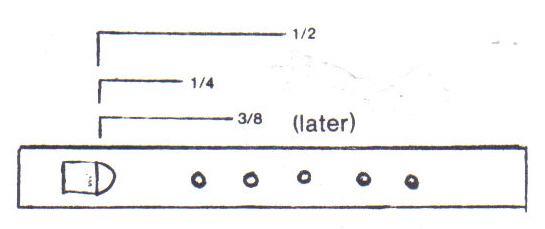
Five of these three-hole flutes were constructed. Later, two more flutes were built with two more holes equidistant between the center and two outer holes.

I also made a flute with three finger-holes spaced according to the "natural" lie of three of my fingers at an arbitrary, but somewhat central, location on the flute. Two of the earlier flutes had finger-holes added according to this procedure with the original center-hole maintaining a position between the two new holes. These two altered flutes had hole distances determined by the right hand of one of my room mates.

Further three sets of pan-pipes were constructed, each consisting of eight bamboo pipes cut consecutively from the natural divisions of the grass. These sets of pipes, each cut from one stalk, were then placed against a wall and arranged in the order in which they came from the plant. The first pipe cut was measured but left unaltered, the last pipe was marked at half the length of the first, and a diagonal line was drawn across the row of eight adjacent pipes from the end of the first, to the point marked on the last. The pipes were then cut at the highest point on each pipe which was intersected by the diagonal line. Thusly:

All the instruments, pipes and flutes alike, were made of bamboo, as this is a readily available tubular material throughout the world. Steel tools were used largely for convenience, the general unavailability of stone cutting tools in Modern America, and my lack of skill with stone tools if they were available. All hole measurements were made with a piece of string approximately an eighth of an inch in diameter, which was folded in half as appropriate to achieve the divisions by half and quarter as required.

This experiment works from the presupposition of a culture without a predetermined scalar-modal system which has the technology to produce fipple-flutes or pan-pipes, and a concept of mathematics and measuring sufficient to derive halves and quarters. Such a culture may have existed in the late Paleo!ithic for all that I have been able to determine. I was interested in finding concurrences with surviving scalar-modal practices, or with Belaiev's theories. I also wanted to determine if fourths and fifths arose from these simple arithmetical relationships.

Methods

As steady as possible tones were blown on the flutes and pipes, trying as much as possible to blow steady fundamentals and avoid over-blowing. These were matched by my ear to sine-wave frequencies produced on Professor F.R. Moore's self-made digital synthesizer, nick-named the FRMbox, at UCSD. When, after a series of attempts of no less than 30 seconds in duration for each note, a subjectively convincing result was achieved, it was written down. As little "beating" as possible between the frequencies produced by the synthesizer and the instruments constituted a convincing result. The FRMbox has an accuracy to 1/6 Hz with a precision of 1 in 2²⁴(16 million-odd) parts.

This question of accuracy versus precision was reflected in other parts of the experiment. While it was possible to determine the precision of cents derived from results of frequency matching, due to the precision of modern pocket calculators, it was very difficult to achieve an accuracy of more than .5 Hz in frequency due to several factors. With these fipple-flutes and pan-pipes it is quite easy to bend the pitches as much as a whole-tone. One also has a temptation, coming from a culture with predetermined scalar-modal systems, and with training or prejudice in those systems, to blow notes which accommodate those systems. Further variations can occur from test to test due to changing humidity and barometric pressure, and the inevitable lack of precision between instruments caused by the primitive measuring system employed. The FRMbox, with its extreme precision and accuracy, is itself subject to fluctuations in current from its regional power-grid. Excluding all of the previous qualifiers, I believe that I at least compensated for my cultural biases to some extent, by the imposition of the 30 second test duration for each note. As I do not possess absolute pitch, this duration affected my tonal memory for long series of pitches on any one instrument.

All frequencies were converted from octal numbers to base ten. Cents were derived following the formula: cents = log₁₀ F₂ / F₁ / 1og ₁₀2 X 1200. The first five fipple-flutes constructed were all tested two times. The latter three sets of fipple-flutes, and the three sets of pan-pipes, were tested only once each due to the sensitivity of the FRMbox to humidity without a permanent home, and the unusually wet weather in California (for the third straight year) during the period of the experiment.

Table 1: 3- and 5-hole Flutes

Italicized numbers are the most relevant to Belaiev's trichordal pentatonic model

Table 2: Flutes with 3 Holes Spaced According to the "Natural" Lie of the Fingers

Italicized numbers are the most relevant to Belaiev's trichordal pentatonic model.

Results

Fingerings for the 3 and 5-hole flutes are shown in tandem to compare the results from isometric hole ratios in proportion to over-all length.

The two flutes (6,7) with 2 holes added according to the "natural" lie of the fingers are included as 3-hole isometric flutes in Table I and as 3-hole "natural" tie flutes in Table II. The following is a list of the symbols and their meanings in Table I.

— = no believable result.'

Lengths are given in centimeters.

Frequencies are given in Hertz.

(1) = first test.

(2) = second test.

x = closed finger-hole.

0 = open finger-hole.

3(+ 2) = 3-hole flutes altered by the addition of 2 holes to equal 3-hole "natural" lie flutes. When they equal these instruments, the outer finger-holes are always closed. Results are in Table II.

My first discovery with the smaller (11.3 to 15.4 cm in length) 3 and 5-hole fipple flutes was that a fourth with an average of 483.6 cents could be obtained with the fingering on the 3-hole flutes, and 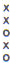(which gives the same hole distance proportions) on the 5-hole flutes. These fourths varied by only 20.5 cents. Apparently though, these fourths apply only to flutes of these approximate lengths and diameters (1.5-1.8 cm) because the two larger 3-hole flutes (20.2-20.4 cm) yielded an average of 381.5 cents with these fingerings. A fingering of 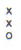( for 5-hole flutes resulted in seconds with an average of 193.6 0 cents for the smaller flutes and 172.8 cents for larger flutes.

The cent values for these seconds and fourths are particularly relevant to Belaiev's theory, yet, these values seem to fluctuate too widely to consistently support his theories. Perhaps only certain size ranges of flutes fall into Belaiev's trichord theory. His theory has another weakness that I observed. None of my instruments could be over-blown at the fourth or fifth to fill out his model of pentatonic scale formation from metrically tempered trichords. I find it unlikely that Belaiev's theory of metric temperament holds water for any wide range of wind instruments, due to the consistency of end pressure regardless of the over-all length of an instrument. Nevertheless, his theory bears considerably more investigation; my study is not broad enough statistically to completely refute his assertions.

Table 3:8-Pipe Pan Pipes

So far as conclusions specifically regarding scalar formation employing the simple fingerings given for isometrically hold 5-hole flutes in Table I, the variations between the individual instruments are rather great. The only consistency I was able to find, within an unacceptably small sample, was a sharp minor sixth with an average of 862.5 cents and a fingering of .

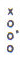The 3-hole flutes spaced according to the "natural" lie of the fingers produced wildly varying results from which no firm conclusions can be drawn. 50 cents constitutes a wide variation from any interval defined as central for the purposes of these experiments. The smallest flute of the previously mentioned group, probably coincidentally, gave results fairly closely in accord with Belaiev's trichord. These three flutes had been constructed to see if the Paleolithic bone flutes (translated to bamboo in these experiments) mentioned by Megaw gave any consistent interval results. There is a possibility of consistency among the paleolithic bone flutes due to the fact that they are generally made from sheep tibia and may, therefore, be of similar size. This makes an assumption of an average hand size (same species or gene-pool of Homo ?), and a consistent placement of the fingers on the bone flutes for measuring purposes. The testing of this hypothesis would involve access to :!l of the bone flutes mentioned by Megaw for measurement; finger placements from a large number of individuals of similar physical characteristics; and access to many tibia from a race of sheep similar to those from which these flutes were constructed!

One coincidence which, for lack of a better term, I will call a pseudo-consistency, involves the fingerings or which divides the flute in half from the front of the fipple to the end of the flute. These fingerings produced thirds averaging 325.9 cents for 3 and 5-hole isometrically spaced flutes, and 318.8 cents for 3-hole flutes with "natural" lie finger placement. The range of the inte^rvals was 241.8 to 410.5 cents. Although this is an extraordinarily large range of cents, perhaps this relates in some way to various theories which claim that chains of thirds are the basis for "primitive" scalar-modal systems.⁵ Apparently divisions by halves are the easiest to make.

The 8-pipe pan-pipes resulted in heptatonic scales closed by near approximations of the octave (1165, 1193.3, and 1223 cents). Although there was considerable variation between the results for each set of pipes, when the gamut of each set was run, the results seem similar to modes or scales that would be familiar to contemporary western listeners. The modes are "minorish"; in a Dorian or Aeolian sense, subjectively.

The use of eight pipes, with the shortest being 1/2 the length of the longest prejudices this experiment in favor of octaves and heptatonic scales, the most familiar types for contemporary western listeners. That intervals close to major seconds are so predominant, (if 160 to 202 cents can be called major seconds), or 15 out of 21 intervals, perhaps aides in achieving this similarity to contemporary scalar-modal systems.

The fact that 9 of 11 instruments produced fourths (460.5 to 511 cents, with an average of ca. 478 cents) would seem to indicate, at least tentatively, that these intervals, along with thirds and seconds, would become readily established in the minds of early instrument makers, using simple, isometric measurements, merely by the frequency of their occurrence.

Summation

Although the production of tones on any of these wind instruments is highly dependent on many variables including air pressure to the instrument from the player to the instrument, barometric pressure, humidity, and cultural conditioning; it appears that certain types of intervals (some seconds, thirds, and fourths) result from simple isometric measurements. How one defines these intervals is dependent upon numerous mathematical models ranging from the ancient Chinese and Greeks, to such near contemporaries as Harry Partch.

Instead of quibbling over the exact number of cents in a fifth, fourth, major of minor third, or second, I propose an approach to future studies of the origin of scales based on generalizations of intervals and scales. In other words, what is more important than levels of preciseness that can only be achieved by the technologies of literate societies, may be the definition and usage of such concepts as "fourth-ness", "pentatonicness", or "diatoniclike". Given that when such a highly sophisticated, theoretically defined pitch artifact as a symphony orchestra plays, the violinist goes sharp during fast, loud passages, while the xylophonist is restricted to a fixed tuning, yet there seems to be a culturally perceptible pitch-system, it seems reasonable to assume that such inconsistencies could be accounted for in comparative ethnomusicological models for scalar-modal systems. Such inconsistencies could be more deeply explored with a large statistical sample derived from the experimental models of this inquiry.

¹Schlesinger, Kathleen, The Greek Aulos. London: Methuen & Co., Ltd.. 1939, p. 37.

² Ibid., p. 75.

³Belaiev, Victor (Belyaev, Viktor). The Formation of Folk Modal Systems. Journal of the International Folk Music Council, Vol. XV, Cambridge, 1963, p. 4.