Music theorists have split personalities. On the one hand, we are creatures of sensibility who got into this field because music touched us very deeply. On the other hand, we are also creatures of reason who try to cultivate careful observation, precise method, solid research, and systematic rigor. Depending on personal temperament and previous experience, each of us leans more to one side than the other, but we all experience to some extent the tension between what we might call our inner humanist and our inner scientist. It is hardly surprising, then, that the tension between science and humanism should also emerge occasionally in our public organs of communication. A case in point is the spirited debate published in the 1989 and 1990 issues of the Journal of Music Theory between Douglas Dempster and Matthew Brown on one side, calling for a scientific approach to music theory, and Benjamin Boretz, John Rahn, Nicholas Cook, and Richard Tarushkin on the other side, expressing what I take to be more humanistic convictions.^[2]  I do not intend to reopen that particular debate today, although it is certainly related to my topic. Instead, I want to show how recent scientific discoveries are changing the image of science from within, and how, in some respects at least, science is moving toward humanism.

                        Although we are all familiar enough with the broad outlines of the conflict between humanism and science, I want to situate one of the sides firmly within music theory, in order to relate the general issues more easily to our own activity.       

                        For this purpose let us take Schenker as an example of extreme music-theoretical humanism. That he should be placed on the humanist side is suggested by the following aphoristic remark from Free Composition: "Music is everywhere and always Art: in composition, in performance, even in its history; but nowhere and never is it Science.''^[3] Moreover, although Schenker developed some powerful analytical generalizations, he used analysis ultimately to illuminate the individual and unique in an artwork, that which cannot be predicted by any universally applicable theory. This commits him to a stance that might be called singularism: the conviction that explanations of artworks must take into account irreducible singularities that cannot be encompassed by universal laws or generalizations - a position that is, I think, in line with our humanistic instincts.

                        What makes Schenker's humanism extreme, however, is that he combined singularism with an organicism that may even list toward anthropomorphism. I want to single out just two aspects of Schenker's organicism that most of us seem to regard as extreme  or unacceptable.

                        First, because a multi-layered analysis represents a kind of development or growth from embryonic elements in the background to fully mature composition in the foreground, Schenker's method suggests teleology or final cause. That is to say, the foreground can be understood as the goal or end toward which the voice-leading transformations strive, much as the fully formed human individual is the goal or final cause of the growth process.

                        Second, because the various parts of the analysis that come into being through the voice-leading transformations could not engage in a concerted development toward a single goal without a principle of coordination, Schenker's approach implies some sort of vitalism.  At the very least, since phenomena analogous to "communication"  - like concealed repetition - occur among and within levels, the parts must have some ability analogous to "perception" in order to take account of, and adjust themselves to, the other parts and the whole.

                        For the sake of this discussion, it will be sufficient to use these three principles found in Schenker's thought - namely singularism, final causality, and vitalism - to represent the extreme pole of humanism.

                        At the opposite pole, we have classical science - that is, science as understood in the West until very recently. Classical science held assumptions that countered all three of the humanistic principles just mentioned.

                        Science opposed singularism by insisting that its form of explanation rested on universal laws or law-like generalizations. Obviously, such generalizations exclude singularities from the outset. Consequently, scientists had to leave discussion of unique and particular aspects of the world to non-scientists.  In the main, they were happy to do so, since their approach provided a clear decision-procedure based on predictivity, which arises directly out of the principle of universality.  Because science's generalizations were supposed to be universal, they had to apply not only everywhere, but also at every time; if a generalization is really universal, then it should cover all possible cases, both in the past and in the future. Now retrodiction is always open to suspicion, because past facts can be rationalized to provide justification for almost any theory. But an accurate model of the future cannot be the product of rationalization; its confirmed predictions must be due to correspondence between theory and reality. So predictivity became the principal test of scientific theory: if a theory failed to predict accurately, then that alone was proof of its inadequacy. The primary manifestation of science's opposition to singularism was its insistence on predictivity.

                        Classical science also opposed final causality and vitalism. For just as Schenker's commitment to these two principles stemmed from a fundamental belief in organicism, science's rejection of them stemmed from a fundamental belief in mechanism. Perhaps the best way to approach mechanism is through an analogy.

                        Imagine a pool table on which a few dozen billiard balls are in constant motion. Imagine further that the tabletop offers no resistance to the motion of the balls, and that the bumpers are perfectly elastic, so that no energy is lost when the balls bounce on the edge of the table. This is an image of a mechanistic system. Everything that happens in this system happens as the result of mechanical action and contact - one ball hits another, which speeds up, bounces off the edge, hits two others, and so forth. From this image we can elicit the fundamental assumptions which gave rise to science's disdain for final causality and vitalism.

                        First,  because every new event in a mechanistic system happens through some sort of contact, the cause of every event is to be sought only in the various contacts that preceded, and resulted in, the event. This is called efficient causality. For instance, if, after numerous collisions, our billiard balls were to line up vertically and move together across the table, the explanation of this curious behavior in terms of efficient causality would be a very complicated account of each ball's activity from the moment motion started until the instant the balls aligned. Notice that an explanation in terms of final cause seems ludicrous in this context. How could we plausibly interpret the concerted motion of the balls as a "goal" toward which the system "strives"?  Who or what would establish such a goal, and how could a bunch of billiard balls strive toward anything? In a thoroughly mechanistic world view, final cause has no role to play; all explanations are based on efficient cause.

                        Second, because events in the system are governed by universal generalizations, the elementary constituents of a mechanistic system are imagined to be inactive and unresponsive materials. It is easy to understand why this must be the case. If the elementary constituents possessed the slightest degree of self-direction, they might not always act in accordance with universal laws, but might make unpredictable motions that would in turn undermine the certainty of efficient causality, since the events could no longer be explained solely on the basis of previous contacts. So mechanistic science had to reject vitalism and prefer materialism.

                        To sum up, then, we now have three pairs of opposites characterizing the contrast between humanism and science: singularism versus predictivity; final cause versus efficient cause; and vitalism versus materialism.

                        I would now like to discuss a few relatively recent discoveries that are pushing contemporary science away from classical science and toward humanism, strange as this may seem to those of us who grew up in an intellectual climate dominated by the assumptions of classical science.

                        A new area of science that has burgeoned in the past two decades is popularly called chaos theory. One of the important discoveries in this field is that the generalizations of classical science are not nearly as universal as was once believed. It seems that almost all the laws of classical science were derived from phenomena that occur in dynamic systems under very special circumstances called equilibrium conditions, among which are the conditions that the total amount of energy in the system remain constant, and that the system be isolated from forces outside the system. Chaos theory has shown that equilibrium conditions are not the normal conditions surrounding natural processes and that the very same dynamic systems that act predictably under equilibrium conditions can also, under nonequilibrium conditions, act in ways that are not just practically, but also theoretically, unpredictable.

                        For instance, example 1 contains three illustrations of a dynamic system devised by Edward Lorenz of MIT to display chaos. This is a schematic of a waterwheel, with square buckets attached to a solid wheel that rotates freely around a central shaft. Each bucket has perforations in its bottom, allowing water to escape. The descending arrows indicate the flow of water, and the curved arrows around the central shafts indicate the direction of spin of the wheel.

 Example 1:  Lorenz's Waterwheel

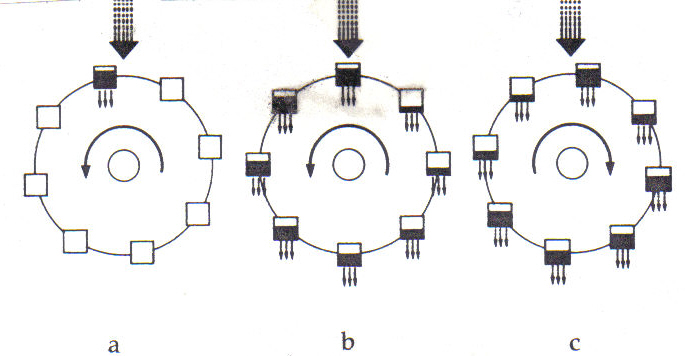
                     Diagram by Adolf E. Brotman in James Gleick's Chaos (New York: Penguin, 1987). Used by permission.

                        If the main flow of water into the topmost bucket is slow, then the water will leak out of the bucket without building up enough weight to overcome the force of friction in the central shaft, and the wheel will not turn at all.

                        If the main flow is increased, though, the top bucket will become heavy enough to overcome friction, and the wheel will begin to move, as is shown in example la. The water will then also begin to fill the other buckets as they come under the flow, and the wheel could adopt a steady rate of motion, as shown in example 1b. The equations for this type of motion are well understood, and, knowing the rate of flow from the tap, the rate of leakage from the buckets, and the coefficient of friction in the central shaft, one can calculate the final speed of the wheel and the position of any point on it at any time in the past or in the future.        

                        If the main flow increases even more, however, the rotation will become chaotic. At a certain point, the amount of water that can accumulate in any one bucket becomes dependent on the speed with which the bucket passes under the main tap. As less water accumulates in some buckets, the other, heavier buckets can start up the other side before they have time to empty, as shown in example 1c. This will cause the spin to slow down, and eventually to reverse. The astonishing fact is that once this behavior has set in, and as long as the flow from the main tap is not decreased, the spin will reverse itself over and over, never settling down to a steady speed and never repeating its reversals in any pattern. This is the signature of chaos.

                        The crucial element in the onset of chaotic behavior is the feedback loop or iteration loop that occurs when processes in a system affect one another: when the wheel spins fast enough so that the amount of water in the buckets affects the rate of spin, which in turn affects the amount of water in the buckets, and so forth, the door is opened for the emergence of chaos. It now appears that such feedback loops are hardly a rarity in nature - in fact, they may be more like the norm - so that chaotic systems seem to be far more prevalent in the world than predictable systems. Scientific research has been energized by this discovery, and the search for chaos has turned up surprises in many different fields - in biology, in physics, in chemistry, in information science, in computer science, in electronics, in the social sciences, even in the stock market analysis. Unpredictability has become very respectable in contemporary science.

                        Obviously, though, unpredictability raises some difficulties for the classical conception of scientific explanation. For one thing, predictivity can no longer play such a large role in determining the adequacy of a theory. If a theory does predict accurately, it may be accounting only for a part of a system's potential behavior; and if a theory does not predict accurately, it may nevertheless be the best account available of an unpredictable phenomenon. In addition, studies in chaos theory indicate that predictability and unpredictability are inextricably intertwined almost everywhere in nature: systems that are predictable on one scale may also be unpredictable on another, or unpredictable systems may nevertheless somehow enfold recognizable patterns in their behavior. This means that unique and unpredictable phenomena are widespread in the world; and, therefore, that a mode of explanation limited to predictive generalizations is far too restrictive to model nature reliably.

                        The current generation of scientists seems to be accepting this last conclusion wholeheartedly. Those who are seeking chaos everywhere have plunged into the realm of the unpredictable with the excitement and energy of explorers who have discovered a new continent. In regard to singularism, I don't think that it is an exaggeration to say that science has finally recognized humanism, and has embraced it.

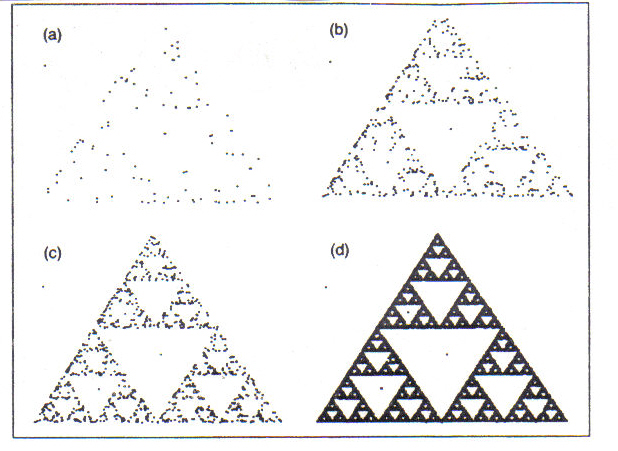
                        The second discovery I want to report on today is also connected with feedback and iteration, and that is the generation of fractal images.  A fractal object is a shape or figure that is composed entirely of transformations of itself at different scales of magnitude. Example 2a is a paradigmatic fractal figure called the Sierpinski gasket. In Example 2b, you can easily see that each of the three large triangles composing the entire figure is a smaller version of the whole, and within each of those triangles there are three smaller versions, ad infinitum.

Example 2: Sierpinski gasket

Enlarged diagram from Heinz Otto Peitgen, Hartmut Jhrgens, and Dietmar Saupe, in Chaos and Fractals: New Frontiers of Science  

(New York: Springer-Verlag, 1992).  Used by permission

                        Figures like this are not so much drawn as they are grown, by many iterations of transformational rules that produce points which are plotted individually on a computer screen. One of the most interesting ways to generate the Sierpinski gasket is the so-called chaos game which shows an intriguing interrelation between randomness and order, reminiscent of the relation between predictability and unpredictability already mentioned. The workings of the game are illustrated in "f" of example 3. First make a die that has two faces labeled 1, two faces labeled 2, and two faces labeled 3. Then, on a surface such as a computer screen, choose three marker points that form a triangle, such as points 1, 2, and 3.  Next, pick a point at random anywhere on the surface; this will be the first game point, z₀ in the example.  Now roll the die.  The next game point will be exactly halfway between the first game point and the marker-point indicated by the roll of the die. So, if the die comes up 2, the new game point will be at z₁ in the example. Continue the game in the same way indefinitely. The example shows the game points selected by six tosses of the die, points z₁ through z₆.

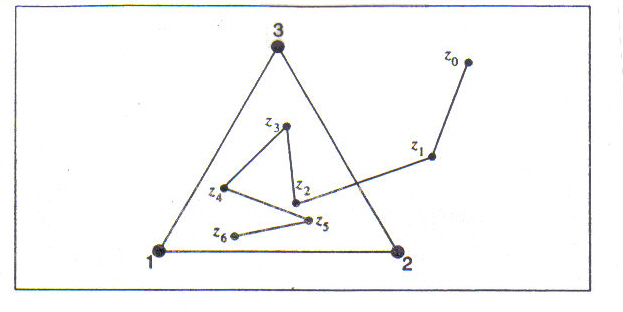
Example 3: Workings of the Chaos Game

                 From Heinz Otto Peitgen, Hartmut Jürgens, and Dietmar Saupe,  in Chaos and Fractals: New Frontiers of Science  

(New York:Springer-Verlag, 1992).  Used by permission

                        Now although the locations of the new game points are completely random, being determined by the roll of a die, the result of many iterations is not random at all. As shown in example 4a-d, the outcome, which becomes clear as more steps are carried out, is the highly ordered Sierpinski gasket. It appears that randomness can combine with rule-based iteration to produce ordered forms. And because all the randomly generated points seem to be drawn toward the figure of the gasket, the latter is called the attactor of this game.

Example 4: Non-random Outcome of the Chaos Game

From Heinz Otto Peitgen, Hartmut Jhrgens, and Dietmar Saupe,  in Chaos and Fractals: New Frontiers of Science  

(New York:Springer-Verlag, 1992).  Used by permission

                        By choosing different base points and different generating rules, the chaos game can he modified to grow an infinite variety of fractal attractors, among which are many natural forms. One of the most celebrated of these games is the one used by Michael Barnsley to generate an attractor shaped like a fern.  Example 5 shows several stages in the growth of the Barnsley fern. It now appears that the shapes of many - perhaps even most - natural objects may be modeled by such attractors.

Example 5: Outcome Stages in Workings of the Barnsley Fern.

Diagram by Michael Barsley in James Gleick, Chaos (New York: Peguin, 1987).  Used by permission.

                                        Since this kind of pattern generation has the look of goal-directed activity, a few scientists seem to be flirting with notions like final causality. It is hard to tell if anyone is taking this matter seriously, because it seems to be absent from the scholarly literature, and there are two good reasons for this.  First, scientists do not, as a rule, concern themselves with metaphysics, and the nature of causality is certainly a matter of metaphysics. Second, the idea of goal-directed activity threatens the mechanistic edifice of science, because, as I have already mentioned, things that can be directed by a goal must somehow be able to sense their relation to the goal, and this implies, at the very least, some sort of perception, if not a rudimentary kind of will. That is to say, admitting final cause raises the specter of vitalism, which classical science rejected out of hand. But I believe that contemporary science will sooner or later have to reevaluate its notions of causality and will have to come to terms with final cause, because, as is shown by the final discovery I want to mention, vitalistic qualities can no longer be completely ruled out in science.

            This last discovery comes from the field of chemistry, and is known as the chemical clock. This phenomenon arises from a feedback situation in a chemical reaction when several reagents are involved in processes that either stimulate or suppress their own production. It turns out that in non-equilibrium conditions, such chemical reactions can develop surprising self-organizational behaviors.

                        One of the most striking of the chemical clocks arises from the so-called Belusov-Zhabotinskii reaction, in which two reagents suspended in a liquid react in a feedback loop that in turn produces a change in the oxidation state of another element. In the case shown in example 6, cesium (III) is transformed into cesium (IV) during one stage in the process, and back again at another stage. This transformation of the cesium atoms produces a change in the liquid's color. The clock faces show that the color changes are regular and periodic: in this experiment, the red changes to blue after 55 seconds, and five seconds later the blue reverts to red.

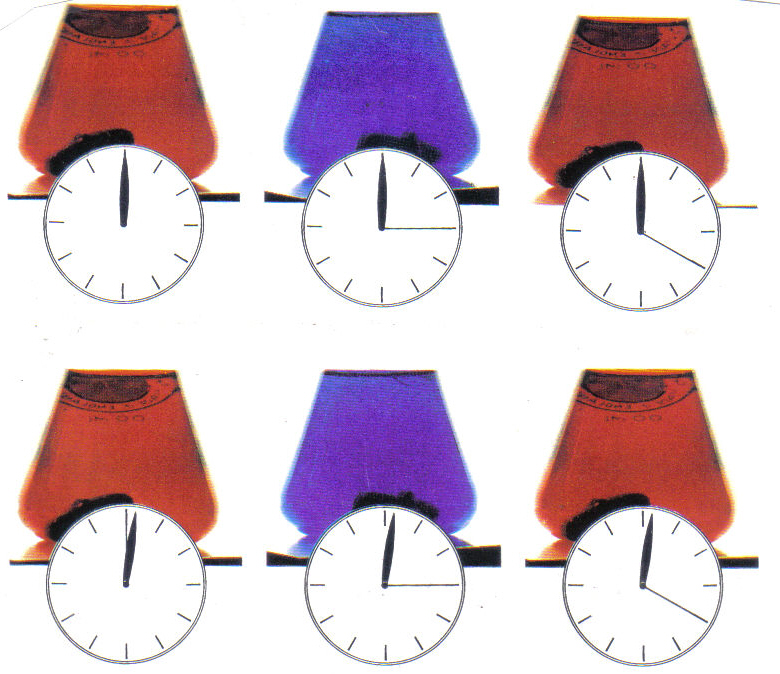
Example 6: Oscillations in the Belousov-Zhabotinskii Reaction

From  Stephen Scott "Clocks and Chaos in Chemistry"  in Exploring Chaos  Nina Hall ed.  (New York: W.W. Norton, 1993).  Used by permission.

                        What surprised scientists about this reaction was the suddenness of the color changes. The traditional picture of chemical reactions - simplifying greatly of course - is that there are millions of molecules and atoms scattered throughout the solution, all reacting randomly. According to this model, a change from red to blue should occur gradually, the solution darkening bit by bit as more and more cesium atoms change state. But that's not what happens. The color changes are instantaneous. It's as if all the cesium atoms are waiting for conditions to be just right. Then, and only then, they all switch their oxidation states in consort.

                        The billiard-ball analogy I used earlier can be applied to this situation. The cesium atoms are like the balls, scattered randomly and wandering around the solution. Their simultaneous transformation from one oxidation state to another is analogous to the billiard balls' suddenly lining up into uniform motion across the table. While such an event might be explicable as a chance correlation of efficient causes acting on inactive materials if it happened only once, or if it happened several times at widely spaced and irregular intervals, the fact that it happens periodically at regular intervals means that the concerted activity cannot be attributed to chance.

                        Indeed, it is difficult to imagine how the atoms in all parts of the solution could coordinate their activity without there being some sort of "communication" among them, or at the very least, some sort of sensitivity to conditions in the surrounding environment that almost has to be described as analogous to "perception." Such a vitalistic notion, of course, would seem completely inappropriate to a thoroughgoing mechanist.

                        Nevertheless, llya Prigogene, a Nobel prize-winning thermodynamicist and one of the boldest speculators among contemporary scientists, has argued for a conception of what he calls active matter. Prigogene believes that the materialist view of matter as inactive and unresponsive may be appropriate only for matter under equilibrium conditions. But in non-equilibrium conditions, he maintains, the elementary constituents of matter must become active; they must become sensitive in some way to conditions outside themselves, so that they become capable of coordinating with one another. Matter, it seems, behaves in two qualitatively different ways: materialistically under equilibrium conditions, and vitalistically under non-equilibrium conditions.

                        Self organizational phenomena - of which the chemical clock is a simple, inorganic example - are forcing science toward recognizing some vitalistic elements in nature. This discovery goes hand-in-hand with the discovery of chaos: science can no longer be satisfied with the constraints of studying only the predictable part of nature or only the material part of nature. And the acceptance of the unpredictable and the vitalistic will, I believe, eventually lead to the rehabilitation of final causality as well, although conditions for that development are not yet propitious.

                        So what does all this mean for music theorists? Well, there are certainly some specific lines of research that might be followed. For instance, it might be profitable to reread Schenker's work with a more sympathetic eye than is customary toward his organicism, with its attendant teleology and vitalism. Or it might be fruitful to investigate whether the growth of fractal attractors has any application to the kind of morphogenetic analysis represented by Schenker's method or by Jackendoff and Lehrdahl's generative theory.

                        But far more important, I think, than any particular research project is this general consequence: science's move toward humanism is the cure for our split personalities. For the tension between science and humanism relaxes once it is understood that predictivity and non-predictivity are not so much characteristics that distinguish scientific explanation from humanistic explanation, but properties of speech that correspond to order and randomness in the world around us. Since order and randomness interpenetrate throughout nature, scientific explanation and humanistic explanation also interpenetrate, as opposite poles of one and the same explanatory activity - the activity of constructing plausible accounts of the way things are. Science and humanism have no borders to protect, nor any boundaries to limit them. So we music theorists, like the new scientists, can search for the general in the particular, or vice versa, as much as we like, without necessarily doing damage to either.

                        Of course, most of us have always pursued our studies in this way, despite any intellectual reservations we may have about crossing putative boundaries between science and humanism, because we know in our hearts that our work requires us to recognize both the general and the particular. As an afterthought, I would like to suggest that our practice of balancing the general and the particular might open up an enticing prospect. We have something of an advantage over the new scientists who are exploring the universe of unpredictability. They are quite unaccustomed to dealing with the unique and the particular, whereas we have a great deal of experience in that area - experience that might be turned into advice if the conditions were right for cooperative work. If science's move toward humanism eventually makes it possible for scientists to really communicate with us, it might not be too farfetched to imagine teams of scientists and music theorists engaged in very exciting interdisciplinary projects. But whether such cooperation will ever come to pass is - l think we must admit - unpredictable.